Wskaźniki klimatyczne - kontynentalizm i oceanizm

Wzajemne oddziaływanie na siebie powierzchni morskich i lądowych odbywa się za pośrednictwem atmosfery. Masy powietrza, transformując się nad tymi zróżnicowanymi pod względem fizycznym powierzchniami, zmieniają swoje właściwości i przenoszą w wyniku działania cyrkulacji atmosferycznej wpływy jednego rodzaju powierzchni nad drugie i odwrotnie, kształtując pewne charakterystyczne cechy klimatu. W najbardziej czytelny sposób, zarówno podłoże oceaniczne jak i kontynentalne, oddziałując na atmosferę, kształtują cechy reżimu termicznego powietrza wyrażonego w rocznych amplitudach temperatury. Cechy reżimu termicznego zaznaczające się w kształtowaniu regionalnej odrębności i zmienności wielkości rocznej amplitudy temperatury powietrza zostały w klimatologii określone mianem kontynentalizmu. Zagadnienie to od ponad 100 lat stanowi przedmiot zainteresowań klimatologów. Stopień kontynentalizmu określa się za pomocą różnego rodzaju wskaźników, które pozwalają dokonać liczbowej charakterystyki wielkości wzajemnego oddziaływania klimatycznego oceanu na kontynent i kontynentu na ocean.

Wskaźniki kontynentalizmu (Continentality Index)

Wskaźniki oceanizmu (Oceanity/Oceanicity index)


Wskaźnik kontynentalizmu termicznego Zenkera (Anna Styszyńska - wszelkie prawa autorskie zastrzeżone)

     Najstarsza próba ilościowego wyrażenia kontynentalizmu została podjęta przez berlińskiego nauczyciela, fotografa, przyrodnika i badacza małżoraczków, dr Wilhelma Zenkera (1829-1899). W 1888 roku opublikował on pracę „Die Vertheilung der Wärme auf der Erdoberfläche” (Rozkład ciepła na powierzchni Ziemi) wydaną przez Verlag von Julius Springer w Berlinie (98 stron), za którą uzyskał nagrodę Akademie des Sciences w Paryżu. W części czwartej (Klimatologischer Theil), w rozdziale 13 (Das Festland. Die Continentalitat – Kontynent. Kontynentalizm, strony 76-82) tej pracy, omawiając kwestie kontynentalizmu Zenker napisał: „powietrze, które unosi się nad kontynentem, przybiera cechy kontynentalne – staje się suche i przy zmieniającym się nasłonecznieniu wykazuje duże wahania temperatury. Gdy powietrze pozostaje nad oceanami, przybiera zupełnie odwrotne cechy – wilgotność i temperatura wykazują niewielkie różnice między zimą i latem. W przypadku powietrza między tymi dwiema skrajnościami można by określić procentowo, jak bardzo ma ono takie lub inne cechy charakterystyczne (kontynentalne, oceaniczne)”.
     Pod koniec XIX wieku pomiary wilgotności powietrza nie były rozpowszechnione, co oznaczało, że do wyznaczenia stopnia kontynentalizmu można było wykorzystać jedynie pomiary temperatury powietrza. Zenker przyjął, że: „stopień, w jakim zmienia się temperatura (zakładając, że wszystko inne pozostaje stałe) jest bezpośrednio zależny od różnicy promieniowania słonecznego między latem i zimą, a różnice te są funkcjami szerokości geograficznej. Teoretycznie aby uzyskać bezpośrednio porównywalne wartości, zakres zmian temperatury (A – amplituda roczna) należy podzielić przez sinus szerokości geograficznej (φ)”. Zenker analizując mapę rozkładu rocznej amplitudy temperatury powietrza na kuli ziemskiej, dostępną w Atlas der Meteorologie Juliusa Hanna (wydany przez Gotha w 1887 roku) stwierdził, że na kontynencie istnieją tylko trzy obszary, których klimat jest nieskażony skutkami ubocznymi. Jednym z takich obszarów są okolice Jakucka i Wierchojańska na Syberii leżące w pobliżu szerokości 65°N, gdzie roczna amplituda temperatury dochodzi do 65°C, drugiem – obszar na północ od Pekinu na szerokości 45°N i trzecim – Sahara w Afryce Północnej, gdzie amplituda temperatury wynosi nieco ponad 20°C na szerokości 18-25°N. Z tego powodu, zdaniem Zenkera, nie wolno dzielić amplitudy temperatury przez sinus szerokości geograficznej, ale przez funkcję, która rośnie szybciej niż sinus od 0° do 90°. Za taką funkcję uznał rzeczywistą szerokość geograficzną (w stopniach), co pozwala dodatkowo na znaczne uproszczenie obliczeń amplitudy względnej: n = (A/φ). Zgodnie z tą zasadą, na podstawie ówcześnie dostępnych danych, Zenker przygotował mapę rozkładu na świecie izolinii amplitudy względnej wyrażonej w procentach  (n = (A/φ) · 100):

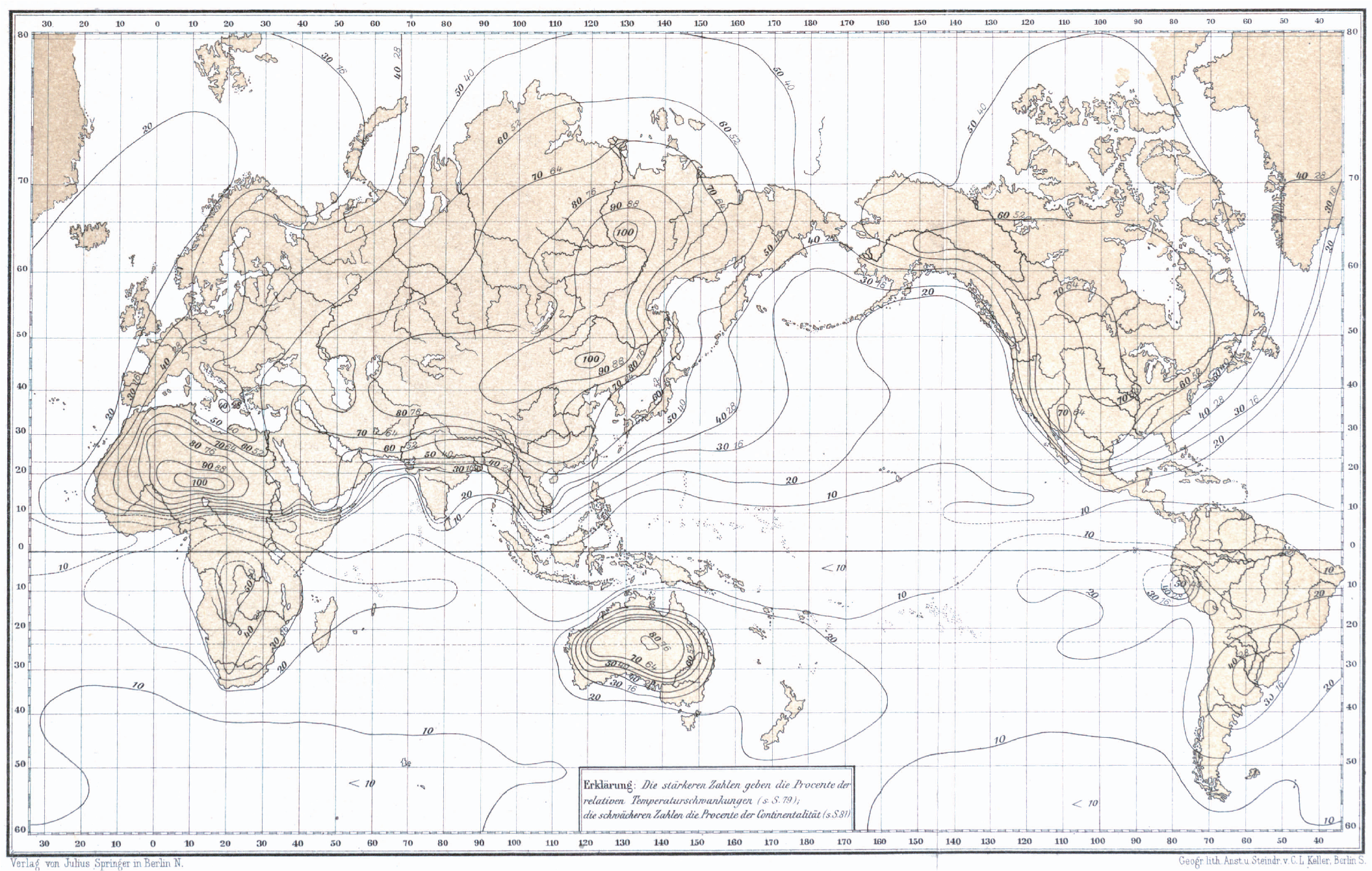
Mapa rozkładu izolinii amplitudy względnej w procentach (duże liczby) wg Zenkera z pracy "Die Vertheilung der Wärme auf der Erdoberfläche" (1888).
Drobniejsze liczby - procent kontynentalizmu

      Po analizie przebiegu tych izolinii nad lądami i oceanami doszedł do wniosku, że wartości amplitud względnych nad oceanami (głównie na półkuli północnej, gdyż rozkład temperatury nad oceanami na półkuli południowej był wtedy słabo rozpoznany) stanowią około 1/6 wartości amplitudy względnej w rejonach centralnych kontynentu (na Syberii). Chcąc zatem ustalić standard kontynentalizmu należy połączyć wartości amplitudy względnej określone dla lądu i morza. W tym celu należy posłużyć się równaniem: K + (100 – K)/6 = n. Po przekształceniu uzyskuje się równanie: K = 6/5 · n – 20, a ponieważ n wyraża się w procentach, to wzór na wskaźnik kontynentalizmu (K) przyjmuje postać:  K (%) = 1,2 · 100 · A/φ – 20.
     W niektórych podręcznikach można znaleźć nieco inne zapisy tego wzoru, nie zmieniające jednak jego sensu liczbowego. Na przykład Wincenty Okołowicz (1906-1979) w "Klimatologii ogólnej" (1969) podaje zapis: K = 6/5 · 100 · A/φ – 20, a Joachim Bluthgen (1912-1973) w pracy „Allgemeine Klimageographie” (1966): K = 600/5 · A/φ – 20.


Wskaźnik kontynentalizmu termicznego Gorczyńskiego (Anna Styszyńska - wszelkie prawa autorskie zastrzeżone)

     Jednym z częściej stosowanych wskaźników kontynentalizmu termicznego klimatu, jest wskaźnik opracowany przez polskiego meteorologa i klimatologa Władysława Gorczyńskiego (1879-1953). Pierwsza wersja tego wskaźnika została przedstawiona w 1918 roku w pracy „O wyznaczaniu stopnia kontynentalizmu według amplitud temperatury” (Sprawozdanie z posiedzeń Towarzystwa Naukowego Warszawskiego, Rocznik XI, z. 4, s. 500-547, 1918). Podstawą do jego wyznaczenia były świeżo wykreślone przez Gorczyńskiego mapy miesięcznych rozkładów temperatury na świecie, opublikowane w pracy „Nowe izotermy Polski, Europy i kuli ziemskiej” (Pamiętnik Fizjograficzny, tom XXV, s. I-VIII + 1-286 + 11 tablic, 1918). Dane do konstrukcji tych map pochodziły dla Europy z lat 1851-1900, dla pozostałych obszarów z różnych okresów, dla których znane były wyniki obserwacji.
     Na podstawie tych map, dla każdego miesiąca, dla kolejnych równoleżników co 5° szerokości geograficznej Gorczyński wyznaczył 36 wartości temperatury odczytanych na przecięciach równoleżników z południkami w odstępie co 10 stopni. Następnie dla każdego równoleżnika obliczył amplitudy roczne (zamieszczone w tabeli 1 w pracy „O wyznaczaniu stopnia kontynentalizmu …”). Wykorzystując wnioski wynikające z pracy W. Pogorzelskiego („Badania teoretyczne ilości ciepła, otrzymywanych na kuli ziemskiej,  z uwzględnieniem strat promieniowania w atmosferze, Prace Towarzystwa Naukowego Warszawskiego, 15, s. 1-100, 1916) Gorczyński założył, że chcąc uwzględnić zmiany temperatury wynikające z różnic szerokości geograficznej, należy wartość amplitudy rocznej temperatury (A) podzielić przez sinus szerokości geograficznej (φ). Na podstawie wartości A/sinφ uzyskanych dla szerokości 30°S – 65°S, wynoszących dla tej strefy przeciętnie 12, uznał, że dla przestrzeni wodnych amplituda temperatury winna wynosić na danej szerokości Awoda = 12 · sinφ.
     Dalej chcąc określić ilościowy wpływ mas kontynentalnych na wzrost amplitudy temperatury należy najpierw od amplitudy dla lądu (A) odjąć amplitudę dla wody (Awoda = 12 · sinφ), wtedy wskaźnik kontynentalizmu termicznego można przedstawić jako iloraz K = c · ((A – 12 · sinφ) / sinφ)), gdzie c – współczynnik proporcjonalności wyznaczony z warunku, że stopień kontynentalizmu termicznego dla miejscowości o najwyższej obserwowanej amplitudzie wynosi 100%. W tym celu Gorczyński przyjął Wierchojańsk (φ = 67°33’N), w którym wtedy średnia amplituda temperatury (z ówcześnie znanych 21 lat obserwacji) wynosiła 65,9°C (styczeń -50,5°C, lipiec 15,4°C). Przy przyjęciu tych danych wartość współczynnika proporcjonalności wynosi: c = (k · sinφ) / (A – 12 · sinφ) = (100 · 0,924) / (65,9 – 12 · 0,924) = 1,686 = ~1,7. Ostateczny wzór na wskaźnik kontynentalizmu termicznego w funkcji amplitudy temperatury i szerokości geograficznej przyjmuje postać: K(%)  = 1,7 · ((A – 12 · sinφ) / sinφ)) = 1,7 · (A / sinφ) – 20,4 .
     Wzoru nie daje się stosować na równiku lub bardzo blisko niego (wartości K dążą do nieskończoności). Aby wyeliminować tę niedogodność Gorczyński zaproponował przyjęcie dla całej strefy 5°N – 5°S jednej wartości amplitudy = 2 i jednej wartości sinφ = 0,1. We francuskim streszczeniu omawianej pracy („O wyznaczaniu stopnia kontynentalizmu według amplitud temperatury”, 1918) znajdują się mapy pokazujące rozkład kontynentalizmu na świecie, w Europie i Polsce:

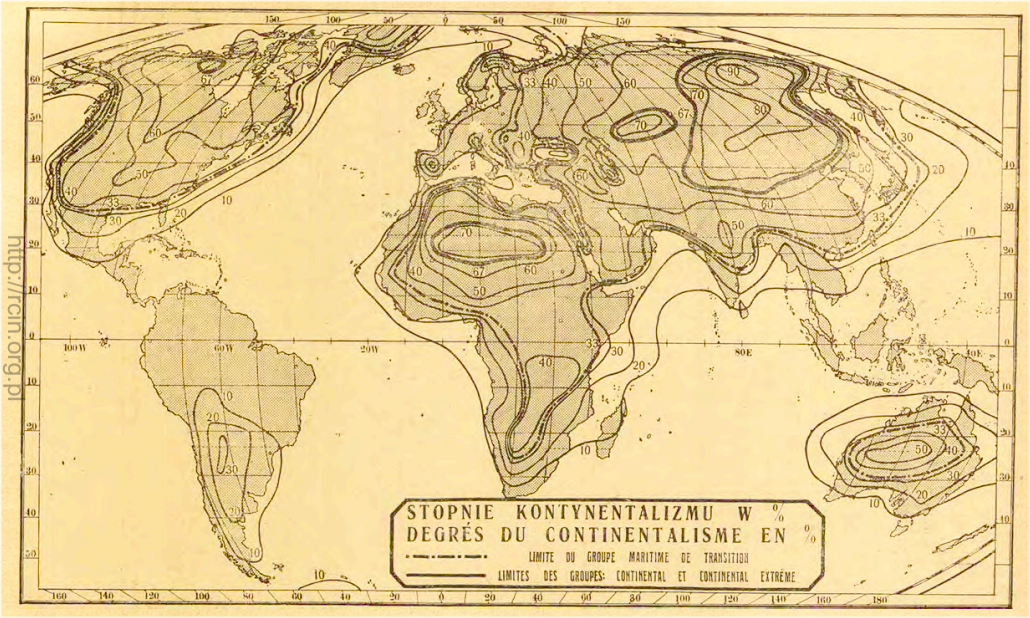
Rozkład kontynentalizmu na świecie wg Gorczyńskiego z pracy „O wyznaczaniu stopnia kontynentalizmu według amplitud temperatury” (1918)

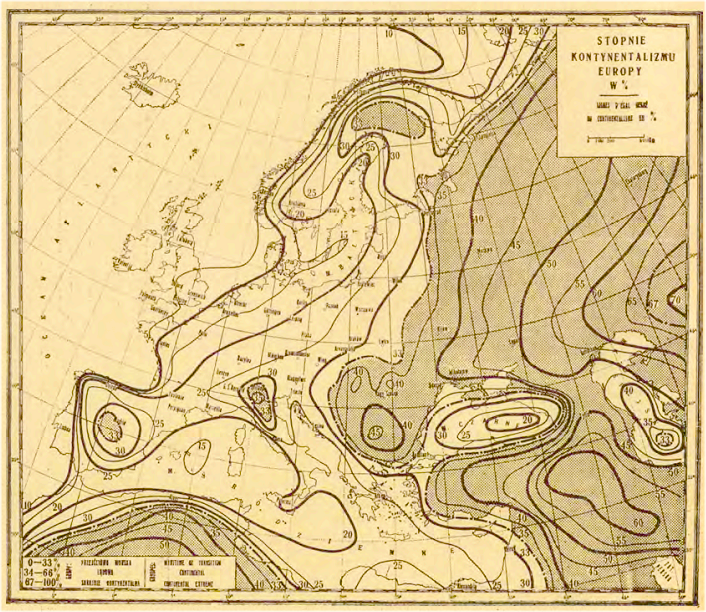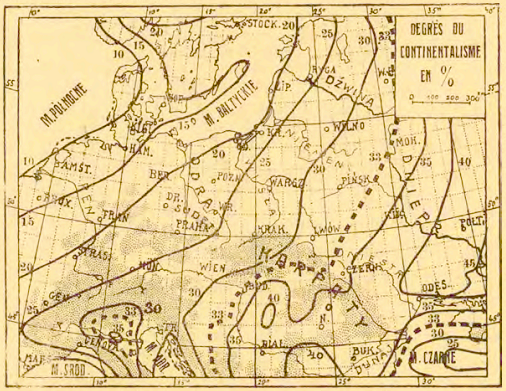Rozkład kontynentalizmu w Europie i Polsce wg Gorczyńskiego z pracy „O wyznaczaniu stopnia kontynentalizmu według amplitud temperatury” (1918)

     Zdaniem Gorczyńskiego wartości kontynentalizmu na morzach utrzymują się blisko 0 (za wyjątkiem wód przyległych do niektórych wybrzeży, np. Azji Wschodniej). Na lądzie wartość kontynentalizmu jest zróżnicowana. Można wyróżnić trzy typy określające stopień wpływu kontynentu na wielkość temperatury:
     1. typ przejściowo-morski – K = 0 do 33%,  2. typ lądowy (kontynentalny) – K = 34 do 66%,  3. typ skrajnie kontynentalny – K = 67 do 100%,
z możliwością dokonania dalszego podziału (np. wyróżniając np. 50 i 85%). Rozkład geograficzny stopnia kontynentalizmu według tych trzech głównych typów, wraz z dwoma podtypami znajduje się na mapie zamieszczonej w pracy Gorczyńskiego „Sur quelques traits caractéristiques du climat de la Pologne parmi les climats européens” (O niektórych cechach charakterystycznych klimatu ziem polskich na tle klimatów Europy, Przegląd Geograficzny, tom 1, zeszyt 1-2, s. 18-50, 1918):

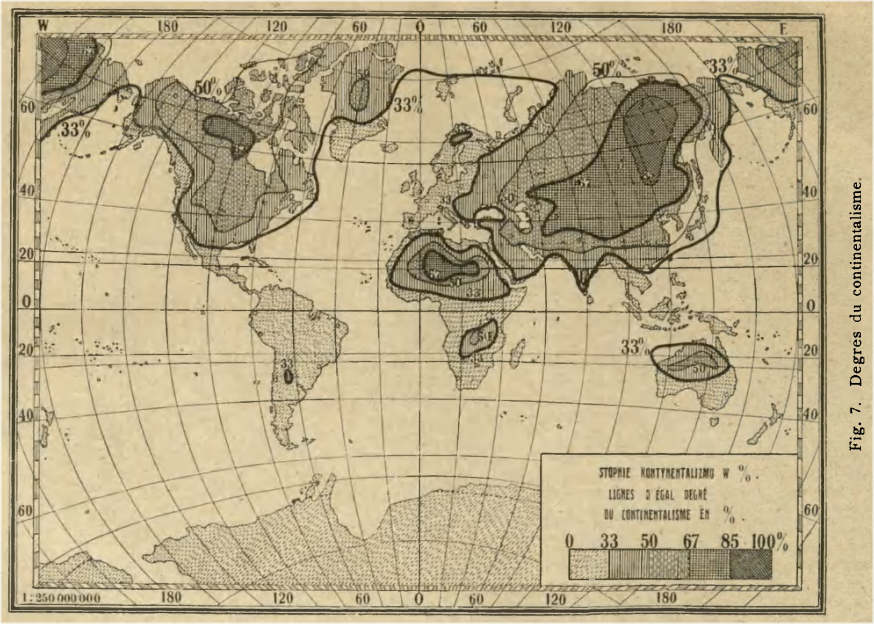
Przebieg izokontynentali rozdzielających główne typy i podtypy kontynentalizmu wg Gorczyńskiego
- mapa z pracy „Sur quelques traits caractéristiques du climat de la Pologne parmi les climats européens” (1918)

      W 1920 roku Gorczyński opublikował pracę "Sur le Calcul du Degré du Continenetalisme et Son Application dans la Climatologie" (Geografiska Annaler, Vol. 2, Issue 4, s.324-331). Zwrócił w niej uwagę na to, że istnieje zauważalna różnica między wartościami amplitudy (A) dla dwóch półkul: półkula południowa wykazuje między 30°S – 50°S znacznie mniejsze amplitudy niż półkula północna. Jeśli zatem ktoś chciałby wziąć specjalną formułę wskaźnika kontynentalizmu dla półkuli południowej, to przyjęcie zamiast A = 12·sinφ wartości: Awoda = 9 · sinφ dałoby lepszą zgodność z obserwacjami:

   Amplituda (A)...    60°S...    50°S...    40°S...    30°S...    20°S...    10°S...
A = 12·sinφ 10,4 9,2 7,7 6,6 4,1 2,1
A = 9·sinφ   7,8 6,9 5,9 5,0 3,1 1,6
Obserwacje 10,5 5,9 5,1 5,4 4,3 1,7


     Przy przyjęciu tych danych i wartości dla Wierchojańska (φ = 67°33’N, A = 65,9°C (styczeń -50,5°C, lipiec 15,4°C) wartość współczynnika proporcjonalności wynosi: c = (k · sinφ) / (A – 9 · sinφ) = (100 · 0,924) / (65,9 – 9 · 0,924) = 1,604 = ~1,6. Ostateczny wzór na wskaźnik kontynentalizmu termicznego dla półkuli południowej w funkcji amplitudy temperatury i szerokości geograficznej przyjmuje postać: K(%)  = 1,6 · ((A – 9 · sinφ) / sinφ)) = 1,6 · (A / sinφ) – 14,4.

     Kilka lat później Oskar Vilhelm Johansson (1878-1956) profesor meteorologii na Uniwersytecie w Helsinkach (Finlandia) w dwóch pracach: trudno dostępnej "Über die Asymmetrie der Meteorologische Schwankungen" (Societas Scientiarum Fennica Communications in Mathematical Physics, Vol. 3, Helsingfors, s. 1-134, 1926) oraz "Die Hauptcharakteristika des jahrlichen Temperaturganges" (Gerlands Beitrage zur Geophysik , Band. 33: s. 406-428, 1931) przyjmując dwie skrajne stacje: najbardziej oceaniczną Torshavn na Wyspach Owczych (φ = 62°N, roczna amplituda temperatury A = 7,6°C), której przypisał 0% kontynentalizmu i najbardziej kontynentalną - Wierchojańsk na Syberii (φ = 67°30'N, roczna amplituda temperatury A = 65,6°C), której przypisał 100% kontynentalizmu, podał formułę określającą stopień kontynentalizmu (degree of continentality): K(%)  = 1,6 · (A / sinφ) – 14. Jest to zapis tożsamy z formułą Gorczyńskiego dla obliczania kontynentalizmu na półkuli południowej. Zdaniem Okołowicza (Klimatologia ogólna, 1969) Johansson nie znał formuły Gorczyńskiego.

     Bardzo podobną formułę przedstawił fiński meteorolog Niilo Raunio w artykule "The Effect of Local Factors on the Meteorological Observations at Torshavn" zamieszczonym w zbiorze prac poświęconym 70-leciu Oskara V. Johanssona (Geophysica, 3, 173-179, 1948). Analizując dane z Thorshavn z okresu 1872-1920 Raunio doszedł do wniosku, że Wyspy Owcze doświadczają wyraźnego efektu kontynentalizmu, i że przy szerokości 62°N nad otwartym oceanem amplituda roczna temperatury powietrza (A) powinna być nieco mniejsza niż w Thorshavn. W świetle danych Raunio amplituda roczna temperatury w Torshavn wynosiła 6,6°C. Po przyjęciu jako drugiej stacji odniesienia, tak jak i inni autorzy, Wierchojańska, Raunio podał swój wzór na obliczanie stopnia kontynentalizmu: K(%)  = 1,57 · (A / sinφ) – 11,7.

Wskaźnik kontynentalizmu termiczno-radiacyjnego Spitalera (Anna Styszyńska - wszelkie prawa autorskie zastrzeżone)

     Rudolf Ferdinand Spitaler (1849-1946) – austriacki astronom, geofizyk i meteorolog – zagadnieniami klimatycznymi zainteresował się pracując jeszcze w Obserwatorium Wiedeńskim. Między innymi w 1887 roku opublikował pracę „Über die Temperaturanomalien auf der Erdoberfläche”– O anomaliach temperatury na powierzchni Ziemi (Petermanns Geographische Mitteilungen, Band 33, s. 364-365), w której przedstawił mapę rocznych izanomal (odchyleń od średniej temperatury równoleżników), a do kolejnej pracy „Über die Temperaturanomalien auf der Erdoberfläche im Januar und Juli” – O anomaliach temperatury powierzchni Ziemi w styczniu i lipcu (Petermanns Geographische Mitteilungen, Band 35, 1889, s. 281-282) dołączył mapy izanomal dla stycznia i lipca. Mapy te stały się podstawą kolejnych prac, realizowanych już w Pradze, gdzie Spitaler został dyrektorem Instytutu Fizyki Kosmicznej i Geodynamiki w Uniwersytecie Niemieckim oraz kierownikiem górskiego obserwatorium do badania fizyki swobodnej atmosfery i stacji meteorologicznej w Donnersbergu (Milešovka, Czechy).
     Pierwsze rezultaty swoich przemyśleń nad różnicami klimatycznymi między regionami kontynentalnymi i oceanicznymi, które uwidoczniły się na opublikowanych wcześniej mapach izanomal, i próbę oszacowania w jakim zakresie rozmieszczenie lądów i mórz wpływa na klimat różnych części powierzchni Ziemi Spitaler przedstawił w pracy (w tej chwili bardzo trudno dostępnej) wydanej własnym sumptem „Das Klima des Eiszeitalters“ – Klimat epoki lodowcowej (Selbstverlag, Prague, stron iv + 138, 1921).
     W rok po ukazaniu się tej pracy Spitaler opublikował jednostronicową notatkę „Klimatische Kontinentalität und Ozeanität” (Petermanns Geographische Mitteilungen, Jahrgang 68, Juniheft, s. 113, 1922), w której podał empiryczną formułę określającą kontynentalizm (n) obliczony na podstawie różnicy temperatury powietrza między lipcem (t'φ) i styczniem (t"φ) oraz różnicy natężenia promieniowania słonecznego w lipcu (S') i styczniu (S"):
n = ((t'φ – t"φ) – 15,94 • (S' – S")) / (130,61 • (S’ – S")).
     W notatce nie podano wyprowadzenia tego wzoru. Jej autor napisał jedynie, że jego podstawą jest – prosty, jak pisze Spitaler – empiryczny wzór określający średnią miesięczną temperaturę powietrza dla równoleżnika o szerokości geograficznej φ: tφ = (-27,37° + 86,78° • So + 15,94° • S) • (1 – n) + (-37,54° + 146,55° • S) • n
gdzie: tφ – średnia miesięczna temperatura na poziomie morza na całym równoleżniku o szerokości geograficznej φ, n – część strefy między szerokościami geograficznymi (φ-1)° i (φ+1)°, która jest pokryta lądem (inaczej względny zasięg lądu na danej szerokości geograficznej), So – średnie roczne natężenie promieniowania słonecznego dla tej szerokości geograficznej, S –  średnie natężenie promieniowania słonecznego dla szerokości geograficznej φ w rozpatrywanym miesiącu.

     Szczegółowego omówienia podstaw konstrukcji formuły określającej kontynentalizm podanej w notatce Spitalera (1922) dokonał David Brunt (1886-1965; pracownik Biura Meteorologicznego Ministerstwa Lotnictwa Wielkiej Brytanii) w 1924 roku w pracy „Climatic continentality and oceanity” (The Gographical Journal, Vol. 64, No. 1, s. 43-49). Omawiając podany przez Spitalera wzór na obliczanie tφ (średniej miesięcznej temperatury na poziomie morza na całym równoleżniku o szerokości geograficznej φ), Brunt zauważył, że jeśli założy się że S = So, to tφ będzie reprezentować średnią roczną temperaturę dla okręgu szerokości geograficznej φ. Gdyby zatem ekstrapolować i przyjąć n = 1, czyli przypadek odpowiadający równoleżnikowi (φ), na którym występuje tylko ląd, to średnia miesięczna temperatura powietrza byłaby określona przez wielkość z drugiego nawiasu w tym wzorze. Gdyby natomiast przyjąć przypadek równoleżnika (φ), na którym nie ma lądów, a tylko ocean, czyli n = 0, to średnia miesięczna temperatura powietrza będzie określona przez wielkość w pierwszym nawiasie omawianego wzoru. Zatem rozkład temperatury nad lądem winien zależeć tylko od S, czyli natężenia promieniowania słonecznego w danym miesiącu, natomiast rozkład temperatury nad oceanem powinien być zależny przede wszystkim od So (współczynnik wynosi 86,78) i w mniejszym stopniu od S (współczynnik 15,94). Zdaniem Brunta wskazuje to na poprawność konstrukcji formuły i jest to zgodne z powszechnie przyjętymi wyobrażeniami co do mocy oceanu do akumulacji ciepła. Temperatura oceanu w ciągu jednego miesiąca jest w dużym stopniu zdeterminowana przez promieniowanie otrzymane w poprzednich miesiącach, podczas gdy ląd szybko wypromieniowuje ciepło i na jego temperaturę w danym miesiącu w niewielkim stopniu wpływa radiacja otrzymana w miesiącach wcześniejszych. Z drugiej strony nie można zdaniem Brunta zakładać, że pierwszy nawias będzie faktycznie podawał rozkład temperatury na półkuli pokrytej wodą, a drugi nawias rozkład temperatury na półkuli tworzonej przez ląd. Jest to według Brunta nieuzasadniona ekstrapolacja, gdyż stałe występujące we wzorze są w pełni określone przez faktyczne rozmieszczenie lądów i mórz oraz faktycznie istniejące osobliwości klimatyczne i nie mają żadnego oczywistego związku ze sztucznymi koncepcjami półkul całkowicie pokrytych lądem lub morzem. Jednakże podstawowym mankamentem tej formuły jest zdaniem Brunta to, że wartość S nie jest mierzona. Została ona obliczona przez Spitalera poprzez porównanie temperatury obliczonej ze wzoru na styczeń, lipiec i rok z wartościami odczytanymi z map rozkładu izoterm dla tych miesięcy, dla kroków 5° szerokości geograficznej pomiędzy 65°N i 55°S i przedstawiona w pracy „Das Klima des Eiszeitalters“ (tabela VI w tej pracy).

     Dalej, jak pisze Brunt (1924), Spitaler założył, że jeżeli znana jest temperatura tφ danego miejsca, to można z niej obliczyć stopień jego kontynentalizmu, czyli wielkość n. Jak Spitaler podaje w pracy „Das Klima des Eiszeitalters“, przeciętny obraz kontynentalizmu uzyskuje się obliczając go ze stycznia i lipca. Jeśli t'φ i t"φ będzie średnią temperaturą, a S' i S" średnią intensywnością nasłonecznienia (promieniowania) odpowiednio w styczniu i lipcu:
t’φ = (-27,37° + 86,78° • So + 15,94° • S’) • (1 – n) + (-37,54° + 146,55° • S’) • n
t”φ = (-27,37° + 86,78° • So + 15,94° • S”) • (1 – n) + (-37,54° + 146,55° • S”) • n
to odejmując od równania lipcowego (t”φ) to ze stycznia (t’φ) uzyska się wielkość n wynoszącą: n = ((t'φ – t"φ) – 15,94 • (S' – S")) / (130,61 • (S’ – S")),
określającą przeciętny (roczny) stopień kontynentalizmu. Taki kształt formuły został podany przez Spitalera w notatce „Klimatische Kontinentalität und Ozeanität” z 1922 roku.
     Trzeba pamiętać, że wpływ lądu i morza na temperaturę powietrza nie jest stały przez cały rok. Ze względu na zmiany przeważającego kierunku wiatru w poszczególnych sezonach, w danym miejscu zimą może wystąpić łagodny klimat oceaniczny, natomiast latem klimat bardziej kontynentalny. Takie efekty mogą się nasilić na obszarach o położeniu zdecydowanie kontynentalnym lub oceanicznym. W pierwszym przypadku wielkość n > 1, czyli klimat będzie bardziej kontynentalny niż na czystej półkuli lądowej, w drugim – wielkość n < 0 – klimat będzie bardziej oceaniczny niż na półkuli oceanicznej. Takie przypadki Spitaler nazwał „nadkontynentalnością” i „nadoceanizmem”.
     Korzystając z tego wzoru oraz map rozkładu izoterm w styczniu i lipcu zamieszczonych w „Atlas der Meteorologie” Juliusa von Hanna (1887), uczeń Spitalera, dr G. Swoboda obliczył wielkości n dla każdego przedziału 5° szerokości i długości geograficznej i wykreślił linie równych wartości n, czyli izokontynentale dla świata i Europy. Ze względu na niepewność obliczenia wielkości n dla rejonu równikowego, gdzie różnice temperatury i natężenia promieniowania (S) są bardzo małe, co powoduje, że wyznaczenie wielkości n w tym obszarze staje się niepewne lub wręcz niemożliwe, na mapie świata w strefie między 20°N i 20°S izokontynentale nie zostały wykreślone. Wykreślone przez G. Swobodę mapy dołączone są do notatki Spitalera z 1922 roku ("Linien gleicher Kontinentalitat und Ozeanitat" Petermanns Geographische Mitteilungen, Jahrgang 68, Tafel 14, 15; 1922). Rozkład izokontynentali na świecie został również dołączony przez Spitalera do jego kolejnej pracy „Linien gleicher Wärme-Ein- und Ausstrahlung und gleichen Kontinentalitätsgrades auf der Erde“ – Linie o tym samym napromieniowaniu cieplnym i promieniowaniu oraz o tym samym stopniu kontynentalizmu na ziemi (Petermanns Geographische Mitteilungen, 1937, Heft 2, s. 33-35 + 3 mapy).

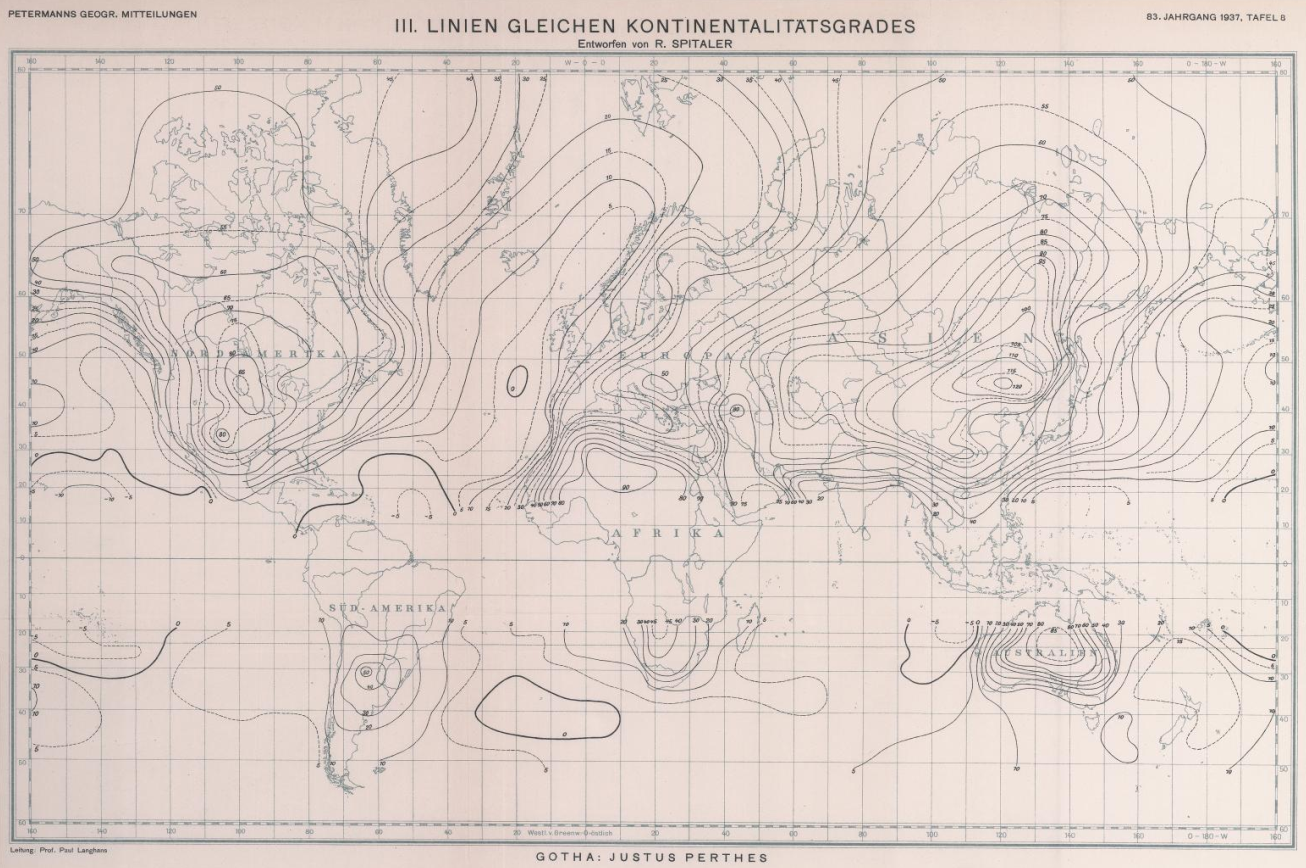Rozkład kontynentalizmu na świecie według R. Spitalera z pracy: Linien gleicher Wärme-Ein- und Ausstrahlung und gleichen Kontinentalitätsgrades auf der Erde (1937)

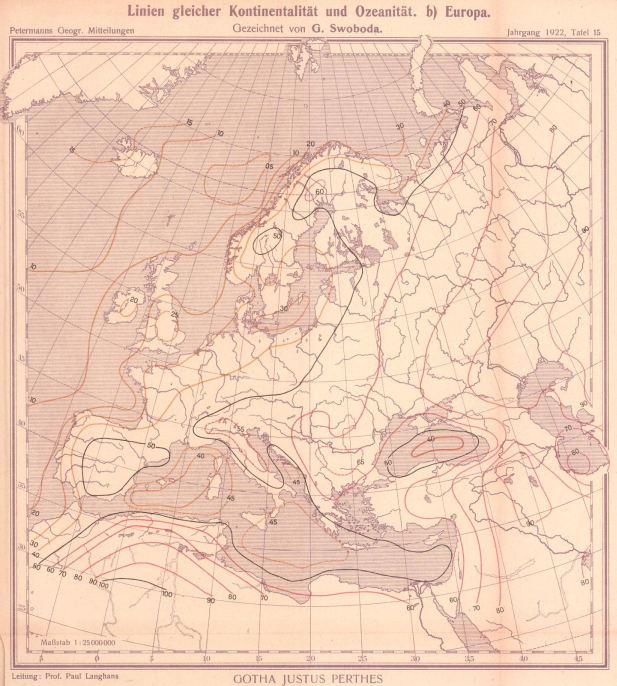
Rozkład kontynentalizmu w Europie według R. Spitalera z pracy: Klimatische Kontinentalität und Ozeanität - Linien gleicher Kontinentalitat und Ozeanitat(1922)

     Brunt (1924) omówił też wzór pozwalający na obliczenie „współczynnika kontynentalnego“ podany przez Spitalera tylko w pracy „Das Klima des Eiszeitalters” (1921). Współczynnik ten, jak pisze Brunt, wyraża ułamek równoleżnika szerokości geograficznej φ, który musiałby być pokryty lądem, aby jako wartość średnią dla całego równoleżnika móc podać różnicę średnich wartości temperatury dla stycznia i lipca występującą w danym miejscu. Obliczyć go można ze wzoru:
ne = (1 / 130,61) • ((t’φ – t”φ) / (S’ – S”)) – 0,12, który można uogólnić do postaci: ne + 0,12 = Δt / 130,61 • ΔS gdzie ne oznacza kontynentalizm, a (ne + 0,12) określa reakcję średniej miesięcznej temperatury powietrza na jednostkową zmianę średniego natężenia promieniowania słonecznego. Wartość ne = ½ oddziela klimat kontynentalny od oceanicznego. Jeśli dla dowolnego miejsca ta reakcja powinna wynosić zero, to odpowiedni współczynnik kontynentalizmu wynosi -0,12.
     Zatem jeżeli Δt określa roczną amplitudę temperatury powietrza, a ΔS – roczny zakres natężenia promieniowania słonecznego na szerokości danego miejsca, to wzór na współczynnik kontynentalizmu może przybrać postać: ne = (A / 130,61 • S) – 0,12. W takiej postaci wzór Spitalera przytacza The Meteorological Glossary, second edition, wydany przez Meteorological Office Air Ministry w Londynie w 1930 roku (na stronie 46) definiując pojęcie kontynentalizmu.

     Do mankamentów formuły Spitalera, poza omówionymi przez Brunta (1924) niewielkimi różnicami między maksymalnymi i minimalnymi sumami radiacji w poszczególnych miesiącach w szerokościach międzyzwrotnikowych, dodać należy jeszcze i ten, że również temperatury stycznia i lipca mogą w tej strefie nie charakteryzować zakresu zmienności temperatury w ciągu roku. Z kolei w szerokościach umiarkowanych, w klimacie oceanicznym półkuli północnej, gdzie występuje przesunięcie maksimum temperatury na sierpień, a minimum – ze stycznia na luty (a nawet na marzec), amplituda roczna obliczona na podstawie temperatury ze stycznia i lipca może być zaniżona. Innym mankamentem takiego podejścia jest to, że promieniowanie słoneczne dochodzące do danego punktu jest obliczane (bez uwzględnienia zmian zachmurzenia), a nie mierzone. Wobec znanego z obserwacji heliograficznych w Europie, znacznego zróżnicowania czasu usłonecznienia na tym samym w przybliżeniu równoleżniku, nie bardzo wiadomo jak obliczane metodą Spitalera wartości (współczynnika?) kontynentalizmu mają się do rzeczywistości.
     Generalnym mankamentem serii prac Spitalera poświęconych kontynentalizmowi jest niejasność terminologiczna (brak zdefiniowania używanych pojęć i wielkości fizycznych, w tym współczynników w poszczególnych formułach), a także używanie wysoce niejasnego mianowania niektórych wartości (np. napromieniowanie wyrażone w °C) – patrz np. tabele w pracy Spitalera „Lufttemperatur und Kontinentalitätgrad” (Petermanns Geographische Mitteilungen, 1936, Heft 1, s. 8-10 + 3 tabele s. 42-45).


Wskaźnik kontynentalizmu termicznego Schrepfera (Anna Styszyńska - wszelkie prawa autorskie zastrzeżone)

     W miarę wzrostu liczby obserwacji meteorologicznych na świecie (w tym na oceanach oraz w głębi kontynentu) zaczęto poprawiać wzór Zenkera. Między innymi niemiecki geograf Hans Schrepfer (1897-1945) w 1925 roku, po analizie danych z okresu 1881-1910 dla 308 stacji zawartych w Hellmanns Klimaatlas von Deutschland (Verlag von Dietrich Reimer, Berlin, 1921) i innych dostępnych ówcześnie danych, w pracy „Die Kontinentalität des deutschen Klimas” (Petermanns Geographische Mitteilungen, 71, s. 49-51), stwierdził, że wartości amplitud względnych nad oceanami stanowią mniejszy odsetek amplitud z głębi kontynentu (które wraz z wydłużeniem okresu obserwacji branym pod uwagę wzrosły) i zmodyfikował wzór Zenkera (K + (100 – K) / 6 = n) używając proporcji 1/8 zamiast 1/6: K + (100 – K) / 8 = n. Schrepfer przypisał wartość K = 0% (klimat morski) Torshavn na Wyspach Owczych i K = 100% (klimat kontynentalny) Wierchojańsku na Syberii. W rezultacie zamiast postaci wzoru Zenkera: K = 600/5 · A/φ – 20 zaproponował: K (%) = 800/7 · A/φ – 14.
     Scherpfer zwrócił też uwagę na wpływ orografii na wielkość kontynentalizmu. Analizując stopień kontynentalizmu na stacjach z obszaru Niemiec zauważył, że stacje położone w obniżeniach terenu i kotlinach górskich, nawet jak leżą na tej samej szerokości geograficznej i tej samej wysokości nad poziomem morza, są znacznie bardziej kontynentalne niż stacje leżące na równinach czy wierzchowinach płaskowyży. Na mapie dołączonej do pracy Schrepfera przedstawiającej rozkład kontynentalizmu na obszarze Niemiec znajdują się dwie tabele pokazujące wpływ orografii na wielkość kontynentalizmu:

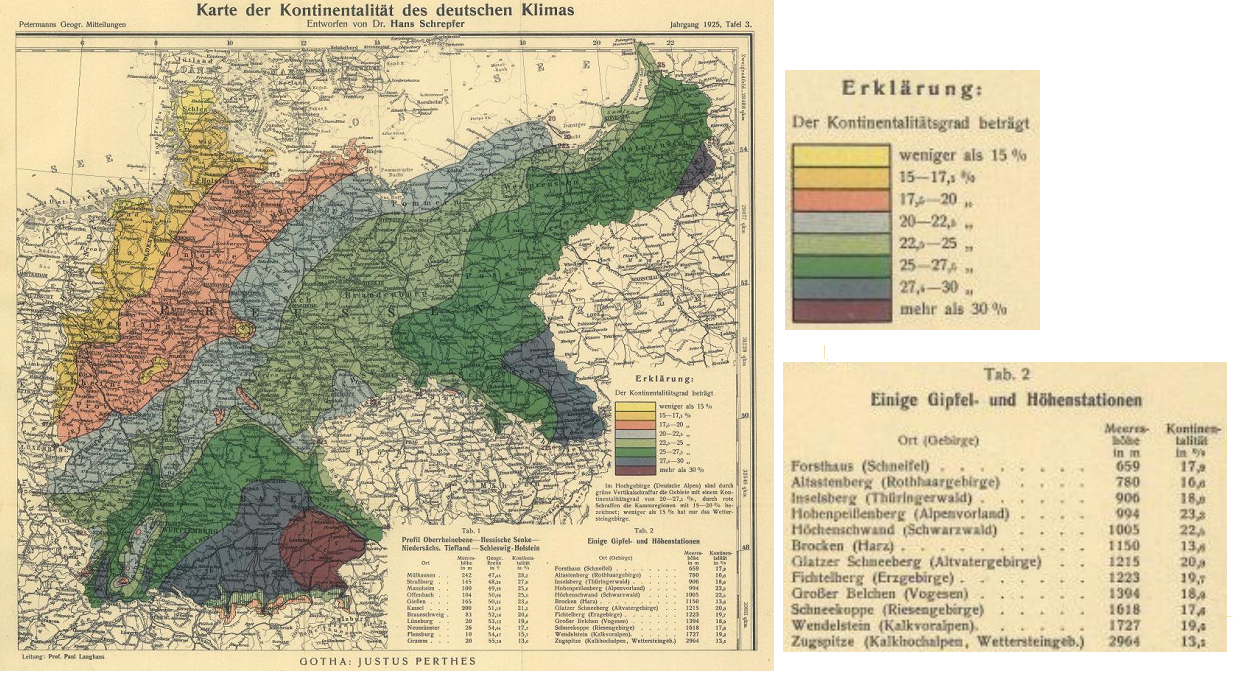
Rozkład kontynentalizmu na obszarze Niemiec wg Schrepfera z pracy „Die Kontinentalität des deutschen Klimas” (1925).
Obok mapy powiększono legendę i treść tabeli 2

     Późniejsze badania innych autorów wykazały ograniczone zastosowanie proponowanych przez Zenkera i Schrepfera wzorów. Między innymi niemiecki geograf Hans Bohnstedt (1907-1966) w pracy „Die thermische Kontinentalität des Klimas von Nordeuropa” (Meteorologische Zeitschrift, Vol. 49, Heft 2, s. 49-62, 1932) wykazał, że wzory te działają dobrze w Europie i ogólnie w szerokościach umiarkowanych, gorzej w szerokościach tropikalnych i stają się bezużyteczne w pobliżu równika, gdzie wartości K dążą do nieskończoności (φ = 0°, dzielenie A przez 0; niebywale wielkie wartości K gdy φ = 0,1-0,3°). Z tego ostatniego mankamentu proponowanych wzorów ich twórcy zdawali sobie oczywiście sprawę już w momencie ich konstrukcji.

Wskaźnik kontynentalizmu termicznego Conrada (Anna Styszyńska - wszelkie prawa autorskie zastrzeżone)

     Austriacko-amerykański fizyk, sejsmolog i meteorolog Victor Anton Conrad (1876-1962) w latach 1936-1946 opublikował kilka prac na temat granic ważności ówcześnie znanych formuł pozwalających oszacować kontynentalizm klimatu. W pracy opublikowanej w 1936 roku – „Die klimatologischen Elemente und ihre Abhängigkeit von terrestrischen Einflüssen“ (w: Koppen W. (ed.), Handbuch der Klimatologie, Band (tom) 1, Teil (część) B, Verlag von Gebrüder Borntraeger, Berlin, s. 376-378) swoją uwagę skupił na analizie wzoru Johanssona (1931). W 1946 roku, w pracy „Usual formulas of continentality and their limits of validity” (Eos, Transaction American Geophysical Union, Volume 27, Issue 5, s. 663-664) swoje rozważania rozszerzył o analizy formuł Zenkera i Gorczyńskiego.
     W tym samym roku ukazał się też jego podręcznik „Methods in Climatology” (Harvard University Press, 254 stron, 1946), w którym Conrad uporządkował i powtórzył swoje dotychczasowe przemyślenia (patrz rozdział XVII, s. 194-198 podręcznika). Wskazał w nich, że wzory określające wskaźnik kontynentalizmu zostały opracowane na podstawie danych dotyczących temperatury zebranych z bardzo ograniczonego regionu równoleżnikowego (głównie szerokości umiarkowanych) i że zastosowanie omawianych formuł do innych regionów jest ekstrapolacją. Wykazał, że dotychczasowe wskaźniki, ze względu na małe amplitudy temperatury w wilgotnym klimacie tropikalnym są trudne do zastosowania w niskich szerokościach geograficznych, i że tracą one swoją ważność, gdy szerokość geograficzna zbliża się do zera. Jako przykład podał stację Kisangani w Zairze (1°N), w której roczna amplituda temperatury wynosi 2,2°C. Zgodnie ze wzorem Johanssona (1931) wykazuje ona współczynnik kontynentalizmu równy prawie 450%, a więc stacja ta miałaby charakteryzować się wpływami kontynentalnymi prawie 4 razy większymi niż w Wierchojańsku, gdzie kontynentalizm wynosi 100% (Conrad 1936). Podobne wyniki Conrad (1946) uzyskał dla 72 innych stacji leżących między 12°N i 12°S, przy czym wyniki te były niezależne od lokalizacji stacji, czy to w głębi lądu, na wybrzeżu czy na wyspie. Na tej podstawie stwierdził, że w rejonach równikowych wpływ szerokości geograficznej na wartość wskaźnika K jest tak silny, że przytłacza wszystkie inne czynniki, a zatem wartości kontynentalizmu uzyskane w pasie między 10° N a 10° S, są niereprezentatywne dla rzeczywistego stopnia wpływu kontynentów stwierdzonego w tych lokalizacjach.

     W podręczniku „Methods in Climatology” Conrad (1946) podkreślił, że opracowując empiryczną formułę kontynentalizmu, należy, o ile to możliwe, wziąć pod uwagę następujące warunki brzegowe:
(1) kontynentalizm uzyskany dla typowej stacji kontynentalnej wyższych szerokości geograficznych musi wynosić około 100,
(2) kontynentalizm uzyskany dla typowej stacji morskiej wyższych szerokości geograficznych musi wynosić około 0,
(3) kontynentalizm typowej stacji morskiej w wewnętrznym pasie tropikalnym musi wynosić 0,
(4) kontynentalizm typowej stacji kontynentalnej w pasie tropikalnym powinna wynosić około 100, jeśli oczywiście na podstawie wszystkich faktów wybrana stacja rzeczywiście wydaje się być czysto kontynentalna. Ponieważ spełnienie wszystkich czterech warunków jednocześnie wydaje mu się niemożliwe, to proponuje przyjęcie założenia, że:
(5) zasięg kontynentalizmu na średnich szerokościach geograficznych musi być wiarygodny; tj. (a) wartości poniżej 0 lub powyżej 100 są niemożliwe, (b) typowe stacje morskie muszą mieć kontynentalizm rzędu 0% oraz (c) stacje czysto kontynentalne, jeśli takie istnieją, muszą mieć kontynentalizm w przybliżeniu równy 100%.

     Po sformułowaniu powyższych założeń Conrad (1946) zmodyfikował formułę Johanssona (1931) tak, aby uzyskać realistyczne wyniki dla niższych szerokości geograficznych. Osiągnął to poprzez dodanie 10° do szerokości geograficznej: K = ((1,7·A) / (sin(φ + 10°)) – 14, gdzie K to kontynentalizm, A to różnica pomiędzy średnią temperaturą najcieplejszego i najzimniejszego miesiąca w stopniach Celsjusza (amplituda roczna), a φ to szerokość geograficzna stacji w stopniach.
Dzieląc roczną amplitudę temperatury (A) przez sin(φ + 10°) Conrad nie tylko zredukował roczną amplitudę do równości dla wszystkich szerokości geograficznych, ale rozwiązał również problem nieokreśloności funkcji w odniesieniu do rejonów równikowych. Pomnożenie średniej rocznej amplitudy temperatury przez 1,7 i odjęcia 14 od 1,7·A/sin(φ + 10°) powoduje, że wartości K uzyskane dla dwóch wybranych stacji, reprezentatywnych dla granic formuły, wyniosą około 100% (Wierchojańsk 99,2%) i około 0% (Torshavn -0,4%) i rozsądne wartości dla strefy okołorównikowej.
     Główną wadą tego wzoru jest to, że formuła traci ważność na szerokościach przekraczających 80° gdyż jeżeli sin90° = 1, to dla dowolnego φ > 80° sinus kąta szerokości dla tej stacji (sin(φ + 10°)) musi być większy niż jeden, a zgodnie z twierdzeniem sinusów jest to niemożliwe. Conrad (1946) stwierdził, że ta wada nie jest zbyt poważna, ponieważ bardzo niewiele stacji meteorologicznych istnieje na szerokościach geograficznych większych niż 80°, zarówno na północy jak i południu.
Ponieważ współautorem drugiego, rozszerzonego, wydania podręcznika „Methods in Climatology” (Second edition. Cambridge, Massachussets, 458 stron), które ukazało się w 1950 roku, jest Leo Wenzel Pollak (1888-1964) – czesko-irlandzki geofizyk i meteorolog (pracujący w Pradze i Dublinie) – to w różnych nowszych opracowaniach dotyczących kontynentalizmu klimatu czasami wskaźnik Conrada nazywany jest indeksem Conrada-Pollaka i cytowany jest za drugim wydaniem podręcznika (1950).


Wskaźnik kontynentalizmu termicznego Heli (Anna Styszyńska - wszelkie prawa autorskie zastrzeżone)

     W 1953 roku fiński meteorolog, oceanograf i geofizyk Ilmo Hela (1915-1976) opublikował pracę „Regional distribution of the continentality in the climate of the oceans" (Geophysica, 4 (2), s. 41-47), w której zaproponował modyfikację wskaźnika kontynentalizmu Conrada. Podstawą przemyśleń Heli były przedstawione przez Conrada w podręczniku „Methods in Climatology” (1946) warunki brzegowe jakie winny być brane pod uwagę przy opracowywaniu empirycznych formuł kontynentalizmu i stwierdzenie, że znane do tej pory wskaźniki kontynentalizmu tylko częściowo spełniają poszczególne warunki Conrada. Zdaniem Heli formuły Gorczyńskiego (1918) i Johanssona (1931) spełniły tylko dwa pierwsze warunki (1 - kontynentalizm uzyskany dla typowej stacji kontynentalnej wyższych szerokości geograficznych musi wynosić około 100, 2 - kontynentalizm uzyskany dla typowej stacji morskiej wyższych szerokości geograficznych musi wynosić około 0), a we wzorze Conrada (1946) uwzględniony został 3 warunek (kontynentalizm typowej stacji morskiej w wewnętrznym pasie tropikalnym musi wynosić 0) i tylko do pewnego stopnia 4 warunek (kontynentalizm typowej stacji kontynentalnej w pasie tropikalnym powinna wynosić około 100). Według Heli nie wydaje się możliwe oszacowanie kontynentalizmu obszaru kontynentalnego w wewnętrznym pasie zwrotnikowym w tej samej skali, co kontynentalizm wyższych szerokości geograficznych. Z tego powodu kontynentalizm podany dla pasa tropikalnego być może zawsze będzie nieco arbitralny. Dodatkowe warunki dotyczące wiarygodności zasięgu kontynentalizmu podane przez Conrada w „Methods in Climatology” (1946) należy wykorzystywać do kontroli nowych formuł wyprowadzanych empirycznie. I choć indeks Conrada (1946) zdaniem Heli wydaje się spełniać warunki brzegowe bardzo dobrze, to pojawianie się nowych materiałów obserwacyjnych może sprzyjać nowym podejściom do określania warunków brzegowych stosowanych formuł. Hela stwierdził, że takie nowe podejście można wykonać wykorzystując nowe źródło danych, jakim w opinii Heli, jest „Atlas map klimatycznych oceanów”.

     „Atlas of Climatic Charts of the Oceans” (red. Willard F. McDonald, U.S. Departament of Agriculture, Weather Bureau, Washington) opublikowano w 1938 roku. Do jego konstrukcji wykorzystano około 5,5 miliona obserwacji meteorologicznych wykonywanych na statkach i w portach w latach 1885-1933. Na ich podstawie obliczono wartości średnie poszczególnych elementów meteorologicznych dla pól (gridów) 5° x 5° szerokości i długości geograficznej w strefie 0-60°N Atlantyku i Pacyfiku. W Atlasie, na 78 stronach zawierających 130 map przedstawiono miesięczne rozkłady charakterystyk wiatru (siła wiatru, wypadkowe kierunki wiatru, częstość występowania wiatrów sztormowych, sezonowe średnie prędkości wiatru i częstości występowania ciszy), sezonowe rozkłady częstości występowania mgieł i zamgleń oraz wielkości widzialności poziomej i średniego zachmurzenia ogólnego nieba oraz częstości występowania poszczególnych rodzajów chmur, prawdopodobieństwa wystąpienia opadów stałych i przelotnych oraz burz. Na mapach numer 115-126 przedstawiono miesięczne wartości temperatury powietrza i powierzchni wody morskiej (°F), a na mapach 127-130 sezonowe różnice temperatury powietrza i wody morskiej. Dane dotyczące temperatury podano w postaci cyfrowej:

Mapa przedstawiająca średnie wartości temperatury powietrza i powierzchni wody morskiej (°F) w gridach 5° x 5° szerokości i długości geograficznej w strefie 0-60°N Atlantyku i Pacyfiku w styczniu (Atlas of Climatic Charts of the Oceans, 1938; źródło: https://archive.org/details/CAT31402344)

     Średnie miesięczne mapy rozkładu temperatury powietrza z tego atlasu stały się podstawą modyfikacji wskaźnika kontynentalizmu Conrada przez Helę. W tym celu zastosował następującą procedurę. Najpierw dla poszczególnych pól (gridów) 5° x 5° szerokości i długości geograficznej w strefie 0-60°N Atlantyku obliczył wartości amplitudy rocznej i ich rozkład przestrzenny zobrazował na mapie (Fig. 1 poniżej). Linie przerywane widoczne na tej rycinie (barwa czerwona) odpowiadają minimalnemu wpływowi kontynentów na klimat Oceanu Atlantyckiego. Następnie te minimalne wartości rocznej amplitudy (A) przedstawił w funkcji szerokości geograficznej (Fig. 2 poniżej).

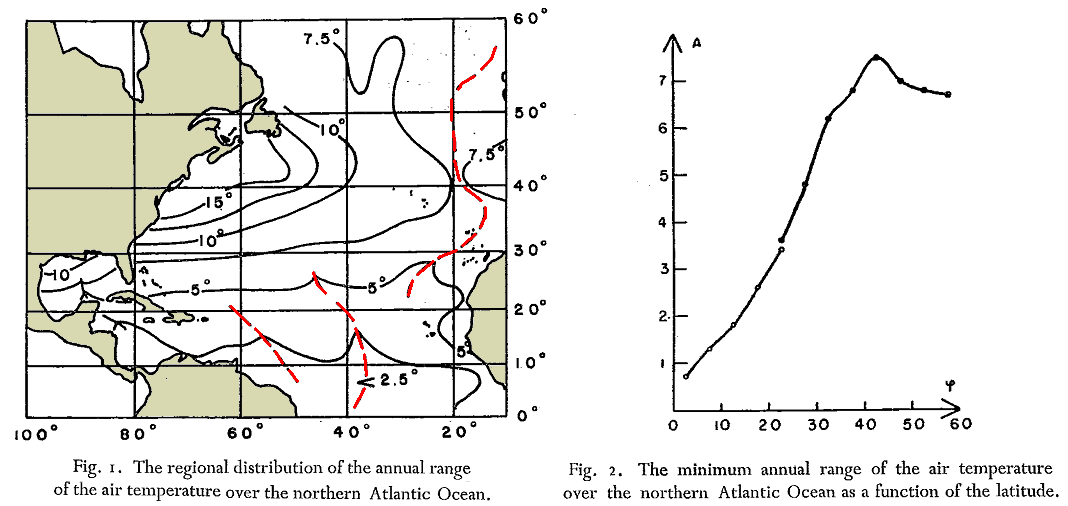
     Metodą najmniejszych kwadratów otrzymał równanie liniowe opisujące zależność minimalnej wartości rocznej amplitudy (A) od szerokości geograficznej (φ): A = 0,13·φ + 0,76. Dalej za pomocą tego równania  Hela obliczył średnie minimalne amplitudy temperatury dla szerokości geograficznej 50° – 7,3°C, 30° – 4,7°C i 10° – 2,1°C. Te trzy wartości razem z amplitudą roczną dla Jakucka (61,6°C) posłużyły Heli do określenia stałych we wzorze typu: K = ((a·A) /(b + sin(φ-φ0)) – d. Wzór ten przyjął postać: K = ((2,2·A) / (0,62 + sin(φ-30)) – 16. Po przeanalizowaniu zakresu zmienności wartości kontynentalizmu (K) obliczonych za pomocą tego wzoru na rzeczywistych danych, Hela stwierdził, że dla dużych obszarów oceanicznych w pasie tropikalnym zachodnich części Atlantyku i Pacyfiku uzyskuje się ujemne wartości, przeczące warunkom brzegowym jakie winny być brane pod uwagę przy opracowywaniu empirycznych formuł kontynentalizmu przedstawionym przez Conrada w „Methods in Climatology” (1946).
     W związku z tym doszedł do wniosku, że zamiast stosować metodę najmniejszych kwadratów, bardziej odpowiednie wydaje się przyjęcie z krzywej minimalnych wartości amplitudy rocznej (przedstawionych na Fig. 2 powyżej) tych wartości, które występują na szerokościach 7,5° (1,3°C), 12,5° ( 1,8°C) oraz 57,5° (6,7°C) i wykorzystać je wraz z amplitudą roczną dla Jakucka (61,6°C) do ostatecznego określenia zależności. W efekcie tych działań wzór otrzymał postać: K = ((1,97·A) /(0,92 + sin(φ-53)) – 13,3, i jak stwierdził Hela po przeprowadzeniu obliczeń sprawdzających, wskaźnik ten z pewnością spełnia trzy pierwsze warunki Conrada z „Methods in Climatology” (1946). Aby zilustrować uzyskane przez siebie wyniki Hela porównał je z wartościami kontynentalizmu obliczonymi za pomocą wzorów Johanssona (1931), Gorczyńskiego (1920) i Conrada (1946). Obliczenia te wykonał dla: typowej stacji kontynentalnej wyższych szerokości geograficznych (Jakuck), typowej stacji morskiej wyższych szerokości geograficznych (Torshavn), typowej stacji kontynentalnej wewnątrz pasa tropikalnego (Elisabethville; 11°39'S, 27°28'E) oraz dwóch typowych lokalizacji morskich: jednej na Atlantyku (2°30'N, 47°30'W) i drugiej na Pacyfiku (27°30'N, 132°30'W):

Stacja      A      Johansson   
 Gorczyński 
  Conrad      Hela   
Jakuck  61,8°C  105 99 96 100
Thorshavn    7,6°C   1 -6  0   0
Elisabethville    7,5°C  49 43 25  24
2°30'N, 47°30'W    1,2°C  33 26 -5   2
27°30'N, 132°30'W    3,8°C   0 -6 -3   3


     Zdaniem Heli, wyniki obliczania kontynentalizmu, w wyższych szerokościach geograficznych oraz na obszarach kontynentalnych w średnich i niskich szerokości geograficznych, za pomocą jego formuły lepiej spełniają warunki brzegowe („Methods in Climatology”, 1946) niż formuła Conrada. Dodatkowo, Hela stwierdził, że jego indeks bardzo dobrze nadaje się do określania regionalnego zróżnicowania kontynentalizmu obszarów oceanicznych, co zilustrował opracowaną przez siebie mapą rozkładu kontynentalizmu na oceanach, w zakresie od 0° do 60°N (mapa poniżej). Pokazuje ona wielki wpływ klimatyczny kontynentów azjatyckiego i północnoamerykańskiego na roczne wahania temperatury powietrza nad morzem, przy czym wpływ Azji na klimat Pacyfiku obejmuje znacznie większe obszary oceanów niż wpływ Ameryki Północnej na klimat Atlantyku. W rozkładzie wskaźnika kontynentalizmu na obu oceanach wyraźnie zaznacza się też wpływ pasatów.

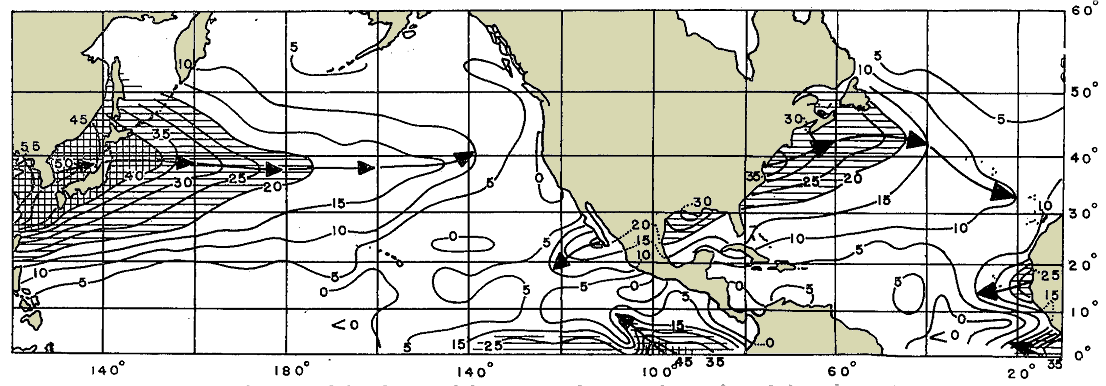
Regionalne rozmieszczenie wskaźnika kontynentalizmu Heli na północnym Pacyfiku i Atlantyku
mapa z pracy „Regional Distribution of the Continentality in the Climate of the Oceans" (1953)

     Omawiana praca („Regional distribution of the continentality in the climate of the oceans”) ukazała się drukiem z rocznym opóźnieniem. Pierwotnie miała zostać opublikowana w 1952 roku (Geophysica Vol. 5, No. 1). Tak też jest sygnowana w innej pracy Ilmo Heli, która dotyczy rozkładu kontynentalizmu w stanie Floryda („Remarks on the climate of Southern Florida” – Bulletin of Marine Science of the Gulf and Caribbean, vol. 2, number 2, s. 438-447, 1952) wydanej przez University of Miami Press. W tej ostatniej pracy Hela wykorzystał opracowany przez siebie wskaźnik do zbadania regionalnego rozkładu kontynentalizmu na lądzie – na Półwyspie Floryda. Wyniki tych badań wskazują, że wskaźnik Heli jest bardzo czuły również w ujęciu regionalnym (Floryda – około 650 km długości, 150 km szerokości, wysokości do 99 m n.p.m.) W świetle badań Heli (1952), w północnej części Florydy kontynentalizm wynosi około 40%, a w południowej – mniej niż 20%. Spadek ten spowodowany jest coraz większą odległością od głównego korpusu kontynentu. Mimo niewielkiej szerokości półwyspu zaznacza się pewne zróżnicowanie wartości wskaźnika między wschodnim i zachodnim wybrzeżem półwyspu (o około 5 jednostek). Asymetria ta związana jest z wpływem wschodniego pasatu.


Wskaźnik oceanizmu Kernera (Anna Styszyńska - wszelkie prawa autorskie zastrzeżone)

     W 1905 roku austriacki geolog i meteorolog dr Fritz von Kerner (1866-1944) w pracy „Thermoisodromen, Versuch einer kartographischen Darstellung des jahrlichen Ganges der Lufttemperatur (Wien)“ - Termoizodromy, próba odwzorowania kartograficznego rocznego przebiegu temperatury powietrza (Wiedeń), opublikowanej w Kaiserlich-Königliche Geographische Gesellschaft (Band 6, Nummer 3, 30 stron + 2 mapy kolorowe) zaproponował metodę ilościowego wyrażania stopnia oceanizmu termicznego opartą o tzw. iloraz termodromiczny q (ang. thermodromic quotient lub thermodromic coefficient).
     Przedstawia on stosunek średniej miesięcznej różnicy temperatury powietrza między październikiem i kwietniem do różnicy między średnimi miesięcznymi temperaturami najcieplejszego i najzimniejszego miesiąca w roku (amplituda roczna temperatury) i przedstawia go w procentach: q = 100 (Toct - Tapr) / A
gdzie: Toct - średnia miesięczna temperatura w październiku i Tapr - średnia miesięczna temperatura w kwietniu (°C), A – amplituda roczna temperatury (°C) - różnica średniej miesięcznej temperatury najcieplejszego i najzimniejszego miesiąca (Tmax - Tmin).
     Opracowując swój indeks oceanizmu Kerner wyszedł z założenia, że w klimacie morskim, ze względu na większą bezwładność termiczną wody (temperatura wody morskiej w październiku jest wyższa niż w kwietniu) jesień jest cieplejsza od wiosny, natomiast w klimacie kontynentalnym wiosna wykazuje wyższą lub zbliżoną temperaturę jak jesienią. Z tego względu różnica średniej temperatury jesieni i wiosny może, obok rocznej amplitudy temperatury powietrza, stanowić dodatkową miarę stopnia „morskości”/„oceaniczności" klimatu.
Jak podaje Czesław Szreffel (Przegląd ważniejszych sposobów charakterystyki stopnia kontynentalizmu, Przegląd Geofizyczny, rocznik 6, zeszyt 3, s. 191-199, 1961), dla uzyskania porównywalności wyników należy obliczyć amplitudę względną współczynnika: a = A / sinφ, a wtedy względny iloraz termodromiczny (Relative thermodromic coefficient) przyjmuje postać: q’ = (100 (Toct - Tapr) / A) · sinφ.
     Na tej podstawie można wyliczyć wartości indeksu oceanizmu, które są bądź dodatnie, bądź ujemne, zależnie od tego, czy jesień jest względnie cieplejsza od wiosny, czy przeciwnie - jesień chłodniejsza od wiosny. Indeks oceanizmu Kernera można stosować tylko w regionach o wyraźnych sezonowych zmianach temperatury powietrza, a takie występują w szerokościach umiarkowanych i wysokich (powyżej 30°). Według Kernera, oceanizm klimatu wzrasta wraz z wartościami wskaźnika. Ujemne lub małe wartości wskaźnika wskazują na wyraźne cechy kontynentalne klimatu, podczas gdy duże wartości (> 10%) wskazują na klimat oceaniczny lub morski.

     Współcześni autorzy do szacowania wpływów oceanu na klimat danego miejsca najczęściej wykorzystują iloraz termodromiczny q. Oznaczają go jako KOI (Kerner's Oceanity/Oceanicity Index) i wyróżniają pięć typów klimatu ze względu na stopień wpływu oceanu na wielkość i zmiany temperatury. Między innymi C. Andrade i J. Corte-Real (Assessment of the spatial distribution of continental-oceanic climate indices in the Iberian Peninsula, International Journal of Climatology, vol. 37, no. 1, pp. 36–45, 2017) czy E. Stonevicius, G. Stankunavicius i E. Rimkus (Continentality and Oceanity in the Mid and High Latitudes of the Northern Hemisphere and Their Links to Atmospheric Circulation, Advances in Meteorology, Volume 2018, https://doi.org/10.1155/2018/5746191) proponują następujące typy klimatu:
     1.  KOI mniejsze lub równe -10 – klimat ultrakontynentalny (hypercontinental),
     2.  KOI od  -9 do   0 – klimat kontynentalny (continental),
     3.  KOI od   1 do 10 – klimat subkontynentalny (subcontinental),
     4.  KOI od 11 do 20 – klimat oceaniczny (oceanic / maritime),
     5.  KOI od 21 do 50 – klimat ultraoceaniczny (hyperoceanic).

     Stonevicius i współautorzy (2018) przedstawiają w swojej pracy rozkład przestrzenny indeksu oceanizmu Kernera (KOI, ilorazu termodromicznego) dla półkuli północnej opracowany na podstawie danych z lat 1981-2010. W świetle ich badań najsilniejszy oceanizm występuje na terenach przybrzeżnych Oceanu Arktycznego, Północnego Atlantyku, Morza Śródziemnego i Dalekiego Wschodu. Najniższe wartości oceanizmu stwierdzono w wewnętrznej części Eurazji (szczególnie w Azji Środkowej i na Wyżynie Tybetańskiej), na kanadyjskich preriach i w Jukonie. Ich zdaniem zależność KOI od średniej temperatury najcieplejszego (Tmax) i najzimniejszego (Tmin) miesiąca jest słaba. Wahania temperatury powietrza w kwietniu odgrywają wiodącą rolę (zwłaszcza w centralnych częściach kontynentów), natomiast temperatury w październiku mają większe znaczenie na obszarach przybrzeżnych. Związane jest to z tym, że o ile nie ma pokrywy śnieżnej, to temperatura powierzchni lądu w kwietniu jest zwykle wyższa niż w październiku na tej samej szerokości geograficznej nad obszarami śródlądowymi.


Wskaźnik oceanizmu Marsza

     W 1995 roku polski geograf i klimatolog Andrzej A. Marsz opublikował pracę „Wskaźnik oceanizmu termicznego jako miara klimatycznego współoddziaływania w systemie ocean – atmosfera – kontynenty” (Wyższa Szkoła Morska, Wydział Nawigacyjny, Katedra Meteorologii i Oceanografii Nautycznej, Gdynia, s. 1-110; streszczenie angielskie – Index of Oceanicity as a measure of climatical interaction in the system ocean – atmosphere – continents), w której przedstawił założenia wyjściowe, zasady konstrukcji i właściwości nowej miary wskaźnika oceanizmu termicznego.

Omawiając założenia wyjściowe konstrukcji swojego wskaźnika A.A. Marsz napisał:
     „ ... Często zapomina się, że około 71% powierzchni planety tworzą morza i oceany. Obszary lądowe stanowią pewnego rodzaju zakłócenie wodnego charakteru powierzchni Ziemi. Lądocentryzm, zrozumiały z punktu widzenia człowieka, jest jednak przyczyną przyjmowania pewnych, zdawałoby się oczywistych, milczących założeń – takich jakie poczyniono przy konstrukcji wskaźników kontynentalizmu – na przykład, że kontynentalizm równy zeru występuje na oddalonych od brzegów lądu obszarach oceanicznych, że tak daleko sięgają wpływy klimatyczne obszarów lądowych. Wzajemna interakcja klimatyczna obszarów lądowych i oceanicznych jest faktem, lecz należałoby postawić pytanie, czy przypadkiem nie jest inaczej – czy oddziaływanie oceanu na obszary lądowe nie jest znacznie większe niż obszarów kontynentalnych na ocean.
     Należy wreszcie zastanowić się czym właściwie jest to co w klimatologii określa się jako KONTYNENTALIZM. Jest to niewątpliwie bardzo skomplikowany zespół cech klimatu, których przejawy znacznie łatwiej określić, niż jednoznacznie zdefiniować samo pojęcie kontynentalizmu. Autor nie jest przekonany, że jednoznaczne, pełne i rozłączne zdefiniowanie kontynentalizmu jako określonego stanu klimatu jest możliwe. … W takiej sytuacji, dalej mianem kontynentalizmu określać się będzie specyficzny stan klimatu, w którym do pewnego, bliżej niejasnego minimum, wygaszeniu ulegają klimatyczne wpływy oceanu.
     Występujące wielkie powierzchnie oceaniczne i morskie, mimo pozornej jednolitości, jednorodnymi nie są, przeciwnie, charakteryzują się istotnym zróżnicowaniem. Zróżnicowanie to szczególnie wyraźnie przejawia się w termice ich powierzchni i jej sezonowej zmienności. Strefowość rozkładu temperatury powierzchni wody jest na wielu akwenach wyraźnie zakłócona, poprzez występowanie systemów prądów morskich, które wraz z adwekcją masy (wód) przenoszą energię (ciepło). Oprócz poziomego przenosu ciepła występuje tu również przenos pionowy masy i energii (zjawiska upwellingów lub zapadania mas wód w głąb – downwelling). Wszystko to razem powoduje, że na obszarach oceanicznych występuje wiele anomalii termicznych, a strefowy rozkład temperatury (i amplitud) stanowi wynik generalizacji.
     Rozpatrywane strefowo amplitudy roczne temperatury wody powierzchniowej, mające bezpośredni wpływ na kształtowanie się amplitudy temperatury powietrza w masach atmosferycznych formujących się nad wodami, wcale nie wykazują wzrostu od strefy równikowej ku biegunom, jak to zakładają W. Gorczyński i S.P. Chromow, lecz maksymalne wartości osiągają w strefie umiarkowanej półkuli północnej (ca 8-10 deg), po czym ponownie ulegają zmniejszeniu w wysokich szerokościach geograficznych (2-3 deg). Na półkuli południowej największe amplitudy roczne temperatury wód powierzchniowych, sięgające 5-8 deg występują w szerokościach 35-40°. Stanowi to głównie odbicie sezonowego zróżnicowania dopływu radiacji do powierzchni oceanu, regulowanego przez zmianę kąta padania promieni słonecznych i długości dnia. Inne czynniki odgrywają rolę istotną lecz podrzędną w stosunku do wymienionych, przez co przy ogólnym omówieniu ich wpływ (np. rozkładu zachmurzenia czy czynnika cyrkulacyjnego) może być pominięty.
     W niskich szerokościach zmiana kąta padania i zmiana długości dnia w ciągu roku jest niewielka, co powoduje brak większego sezonowego zróżnicowania w wielkości dopływającej radiacji. Dopływ radiacji do powierzchni oceanu jest stale duży w związku z czym amplituda temperatury wód powierzchniowych jest minimalna. W miarę wzrostu szerokości geograficznej amplituda temperatury wód powierzchniowych wzrasta bardzo powoli, bardziej skutkiem zróżnicowania długości dnia i zmiany albedo powierzchni w funkcji zmiany kąta padania, niż zmiany natężenia, promieniowania słonecznego. W szerokościach umiarkowanych, sezonowa zmiana kąta padania i sezonowa zmiana długości dnia, powodują bardzo duże zróżnicowanie wielkości dochodzących do powierzchni i pochłanianych sum radiacji w sezonach skrajnych, co znajduje odbicie w dużych amplitudach temperatury wody powierzchniowej.
     W wysokich szerokościach geograficznych zaznacza się jeszcze silniejsza sezonowa zmiana długości dnia, lecz wobec niewielkich kątów padania promieni słonecznych i szybkiego wzrostu w tych warunkach masy atmosfery, przez którą promieniowanie przechodzi nim dojdzie do powierzchni Ziemi, natężenie dopływającej radiacji jest niewielkie, stąd i sumy dopływającej radiacji w sezonie „ciepłym” są niewielkie. Na dodatek, przy niewielkich wysokościach Słońca albedo powierzchni wody jest wysokie, co powoduje, że ilość pochłanianej przez powierzchnię wody radiacji jest wydatnie zmniejszona. Ten ostatni efekt w duże mierze redukuje rolę wydłużonego dnia. Nie pozwala to na wydatniejszy wzrost temperatury wód powierzchniowych w okresie ciepłym i amplituda temperatury wód powierzchniowych jest mniejsza niż w szerokościach umiarkowanych. Należy mieć na względzie, że dolna wartość graniczna temperatury wody jest określona fizycznie przez temperaturę krzepnięcia wody morskiej (~ -1,9°C). O ile w warstwie powierzchniowej oceanu nie występuje silna stratyfikacja zasolenia (wysłodzenie wód), a głębokości są większe, temperatura wód powierzchniowych w sezonie chłodnym będzie bliska temperaturze zamarzania, lecz dzięki konwekcji na ogół nie spada poniżej tej wielkości. Działanie tych czynników powoduje, że w wysokich szerokościach, tam gdzie powierzchnia oceanu nie zamarza, roczne amplitudy temperatury wody powierzchniowej przyjmują wartości zbliżone do amplitud obserwowanych w strefie przyrównikowej.
     Stąd też przyjmowanie jakiejś stałej wartości amplitud dla kuli ziemskiej jednolicie oblanej wodą (jak to czyni W. Gorczyński i jego następcy) stanowi bardzo grube przybliżenie. Zakładanie istnienia jakiejś „czysto oceanicznej amplitudy” temperatury powietrza, jak czyni to S.P. Chromow (1957 – K voprosu o kontinentalnosti klimata) stanowi tylko hipotezę, trudną do zaaprobowania obecnie, gdy istnieją już względnie kompletne i wiarygodne opracowania pomiarów temperatury wody powierzchniowej z materiałów rejsowych dla całej powierzchni Oceanu Światowego i dla wszystkich miesięcy roku (patrz Atlas Okeanov …1974, 1977, 1980). Korekta wpływu szerokości geograficznej na wielkość amplitudy temperatury powietrza przez wyrażenie (C · sinφ), gdzie C stanowi jakąś wartość, mającą charakteryzować wielkość amplitudy nad oceanem (u S.P. Chromowa C = 5,4) powoduje powstanie zasadniczych rozbieżności między oceną „wzorcowej amplitudy oceanicznej”, a przebiegiem rzeczywistym. Przekonuje o tym proste porównanie obliczonych według S.P. Chromowa (1957) wielkości „czysto oceanicznej amplitudy” rocznej temperatury powierza z amplitudami rocznymi temperatury powierzchni Oceanu Światowego, której przebieg amplituda temperatury powietrza nad oceanem, z dala od brzegu, dość wiernie naśladuje (np. na 40°N amplituda powietrza wynosi 3,5 deg, amplituda temperatury wody 10,2 deg).
     W świetle powyższego rysuje się pytanie, czy w ogóle istnieje coś takiego jak „czysto oceaniczna” amplituda temperatur rocznych? Czy istnieje sens poszukiwania normy klimatycznej (wzorca) dla określenia wielkości kontynentalizmu lub oceanizmu na obszarach morskich lub te akweny uwzględniającej? Niewątpliwie istnieje pewien przedział rocznych amplitud temperatury charakterystycznych dla obszarów oceanicznych, nie jest to jednak żadna konkretna, jedynie słuszna, wartość.
     Inaczej przedstawia się sprawa z kształtowaniem się rocznych amplitud temperatury powietrza na obszarach lądowych. Tam podłoże uniemożliwia poziomy przenos ciepła wraz z przenosem masy podłoża, czyli stanowi przeciwieństwo sytuacji występującej na obszarach morskich, na których system cyrkulacji wód jest czynnikiem wtórnej międzystrefowej dystrybucji ciepła przekazywanego do atmosfery, a parowanie ze swobodnej powierzchni wodnej unosi ogromne ilości ciepła utajonego, które następnie przenosi cyrkulacja atmosferyczna. Na takiej powierzchni nie będzie się również obserwować procesów adwekcji ciepła zachodzącego pod działaniem ruchów pionowych substratu podłoża.
     Wewnątrz masywów lądowych, gdzie dochodzą wyłącznie lub prawie wyłącznie masy powietrza przetransformowane w powietrze kontynentalne, na kształtowanie się ustroju termicznego nie będzie wywierało większego wpływu ani ciepło odczuwalne, ani też utajone ciepło kondensacji przynoszone znad powierzchni oceanicznych. Należy się spodziewać, że wielkość amplitudy będzie tam zależna od sezonowej zmienności bilansu radiacyjnego (a więc szerokości geograficznej) i wysokości nad poziom morza oraz trudno definiowalnych czynników lokalnych.
     W świetle powyższego sądzić więc należy, że klimatycznej normy amplitud poszukiwać należy raczej na obszarach lądowych, niż morskich. Z całą pewnością normy takiej nie należy równocześnie poszukiwać na obszarach morskich i kontynentalnych. Jednocześnie w tym konkretnym przypadku, jeśli nie chce się ponownie otrzymać kolejnych map odchyleń od średnich, należy odejść od analizy strefowej, w jej dotychczasowym rozumieniu (średnie dla równoleżników lub stref szerokościowych), skutecznie zacierającej rzeczywiste zróżnicowanie.
     W celu wyznaczenia normy klimatycznej, określającej wielkości amplitud temperatury rocznej należałoby wybrać stacje meteorologiczne zlokalizowane w głębi kontynentu, w miarę możliwości jak najbardziej oddalone od linii brzegowej, reprezentujące wszystkie strefy szerokościowe. Stacje to powinny reprezentować jeden przedział wysokościowy, w miarę jak najniżej położony, tak, aby wpływ zróżnicowania wysokości nad poziom morza na wielkość amplitudy został zminimalizowany. Norma taka stanowić będzie niejako „naturalną” ziemską normę kontynentalizmu.
     Następnym krokiem, pozwalającym na dokładniejsze sprecyzowanie tej normy klimatycznej, jest wyjaśnienie wpływu szerokości geograficznej na kształtowanie się wielkości amplitudy rocznej temperatury powietrza. Warunkiem prawidłowego przeprowadzenia takiej analizy jest jednakowa liczba stacji reprezentujących poszczególne strefy szerokościowe. … Po szczegółowej analizie wybrano 72 stacje o położeniu wewnątrzkontynentalnym leżące w przedziale wysokości od 18 do 385 m n.p.m. reprezentujące Afrykę (15 stacji), Amerykę Północną (12), Amerykę Południową (13), Australię (3) i Azję 29 stacji). Dla każdej 10-stopniowej strefy szerokościowej w przedziale od 0° do 70° skompletowano 10 stacji, dla strefy 70-80° 2 stacje i to położone blisko granicy tej strefy (71°). ...”

     Po przeprowadzeniu analizy związku zachodzącego między szerokością geograficzną (φ) i amplitudą roczną temperatury powietrza (Ar) okazało się, że zależność tą najlepiej oddaje krzywa najlepszego dopasowania będąca wielomianem 4°. Formuła ta objaśnia w 96% zależność Ar = f(φ). Przebieg tej krzywej jest niemal prostoliniowy, pewne nieliniowości zaznaczają się jedynie w strefie szerokości 0-10° oraz 30-50°. Na tej podstawie A.A. Marsz założył, że można zależność amplitudy rocznej temperatury powietrza (Aro) od szerokości geograficznej opisać za pomocą równania liniowego: Aro = 0,775762 · φ – 2,211835. Zależność ta jest zdeterminowana w 93%. Przy założeniu symetrii obu półkul Ziemi można za pomocą tej formuły obliczyć teoretyczną amplitudę temperatury rocznej obszarów wewnątrzkontynentalnych położonych w szerokościach o 0 do 71°. Biorąc pod uwagę liniową zależność Aro = f(φ), można też pokusić się o ekstrapolację tej zależności na strefę szerokości 72-90°. Według tej formuły, gdyby na biegunach znajdowały się kontynenty położone nisko nad poziomem morza (do 365 m), to roczna amplituda temperatury winna wynosić na samym biegunie 67,62 deg. Z kolei dla bardzo niskich szerokości (0-2,8°) wartość Aro będzie przybierać wielkości ujemne (od -2,22 na równiku do -0,046 deg na szerokości 2,8°). Z tego względu dla 10 nisko położonych (18-385 m n.p.m. dla φ = 0-4,3°) stacji wewnątrzkontynentalnych Afryki i Ameryki Południowej obliczono Aro = 1,767°C i przyjęto tę wartość jako charakterystyczną dla równika. Prostą przebiegającą przez oba punkty określa równanie: Ao = 0,7317 · φ + 1,767, gdzie Ao – amplitutuda obliczona. Równanie to wyznacza wielkość amplitudy rocznej temperatury w funkcji szerokości geograficznej na obszarach wewnątrzkontynentalnych, od równika do bieguna.
     Jeżeli obliczoną, teoretyczną, wielkość amplitudy Ao podzielić przez rzeczywiście występującą w danym punkcie powierzchni Ziemi amplitudę roczną temperatury (A), to otrzyma się informację, ile razy amplituda obliczona jest mniejsza lub większa od amplitudy rzeczywistej. Wielkość tą A.A. Marsz nazwał WSKAŹNIKIEM OCEANIZMU (Oc):
Oc = Ao / A = (0,732 · φ + 1,767) / A, gdzie: φ – szerokość geograficzna stacji, A – roczna amplituda temperatury powietrza [°C].
     Wielkość Oc jest niemianowana i w przypadku Ao = A będzie przybierać wartość równą 1, w każdym przypadku gdy Ao < A mniejszą od 1, a w każdym przypadku gdy Ao > A – większą od jedności. Ponieważ Ao jest zawsze dodatnie, to wskaźnik Oc nie może być ujemny. Skoro wielkość Ao posiada wyłącznie strefowy charakter, to wszelkie odchylenia od idealnie strefowego układu amplitud temperatury winny ujawniać się w wartości wskaźnika Oc.

     Do wyskalowania bezwymiarowego wskaźnika Oc A.A. Marsz wykorzystał kilkaset stacji meteorologicznych z całego globu, dla których obliczył wskaźnik oceanizmu Oc oraz indeksy kontynentalizmu według W. Gorczyńskiego oraz S.P. Chromowa. Przeprowadzone porównania pozwoliły na wyróżnienie w występującej na Ziemi zmienności wskaźnika oceanizmu Oc 5 typów (kategorii) klimatu:
           Oc > 3,99 – klimat ultraoceaniczny
         3,99 – 3,00 – klimat oceaniczny
         2,99 – 2,00 – klimat suboceaniczny
         1,99 – 1,00 – klimat kontynentalny
           Oc < 1,00 – klimat ultrakontynentalny
Określenie wartości wskaźnika Oc z dokładnością dwu miejsc po przecinku powoduje, że w każdym typie klimatu występuje gradacja w częściach setnych, pozwalająca na dokonywanie względnie czytelnych porównań natężenia oceanizmu. Wskaźnik oceanizmu Oc jest stosunkowo czułym narzędziem, wyraźnie reagującym na nawet minimalne zmiany amplitudy temperatury i szerokości geograficznej (patrz na ryc. 4 i 7 w omawianej pracy – poniżej – pokazujące rozkład przestrzenny Oc na obszarze Polski i Arktyki). Wskaźnik Oc może być stosowany nie tylko do badań przestrzennych, ale również do badań szeregów czasowych.

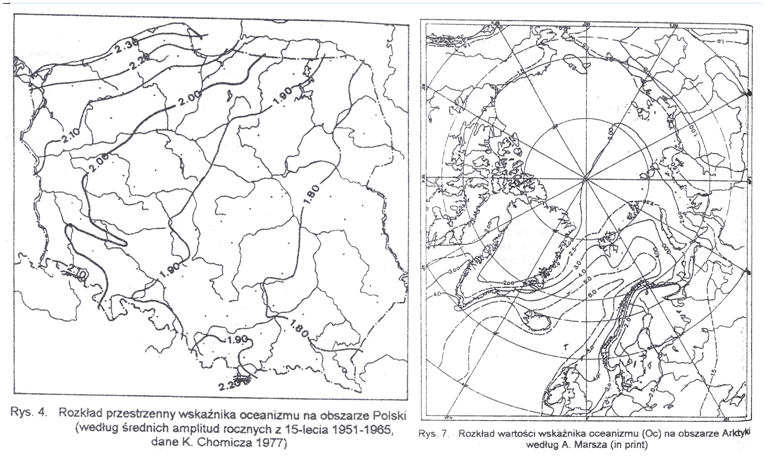Rozkład przestrzenny wskaźnika oceanizmu na obszarze Polski (według średnich amplitud rocznych z 15-lecia 1951-1965, dane K. Chomicza 1977) – po lewej
oraz na obszarze Arktyki – po prawej

     W celu uzyskania orientacji jak kształtuje się rozkład wskaźnika Oc w skali globalnej A.A. Marsz opracował mapę (patrz poniżej) jego rozkładu. Do konstrukcji mapy wykorzystał dane z około 970 stacji lądowych, a dla obszarów oceanicznych dane wyinterpolowane dla punktów węzłowych siatki siatki geograficznej 5° x 5° z miesięcznych map rozkładu temperatury powietrza zamieszonych w „Atlasach Oceanów” (1974 – Tikhij Okiean, 1977 – Atlanticeskij i Indijskij Okieany oraz 1980 – Severnyj Ledovityj Okiean). Na mapie przedstawiono izolinie rozdzielające główne kategorie klimatu (co 1,00). W obrębie klimatu kontynentalnego wykreślono dodatkowo izolinię 1,50, a w obrębie klimatu ultraoceanicznego dodatkowe izolinie 6,00, 8,00, 10,00 oraz 12,00, co pozwoliło przedstawić pewne osobliwości w kształtowaniu się wskaźnika Oc. Na obszarach kontynentów rozkład wskaźnika Oc jest w znacznej części zgodny z rozkładem różnych wskaźników kontynentalizmu (za wyjątkiem S.P. Chromowa). Na mapie zwraca uwagę występowanie obszarów klimatu kontynentalnego i ultrakontynentalnego nad obszarami morskimi. Taki rozkład wskazuje, że wskaźnik Oc co innego charakteryzuje nad powierzchniami lądowymi, a co innego nad powierzchniami morskimi.



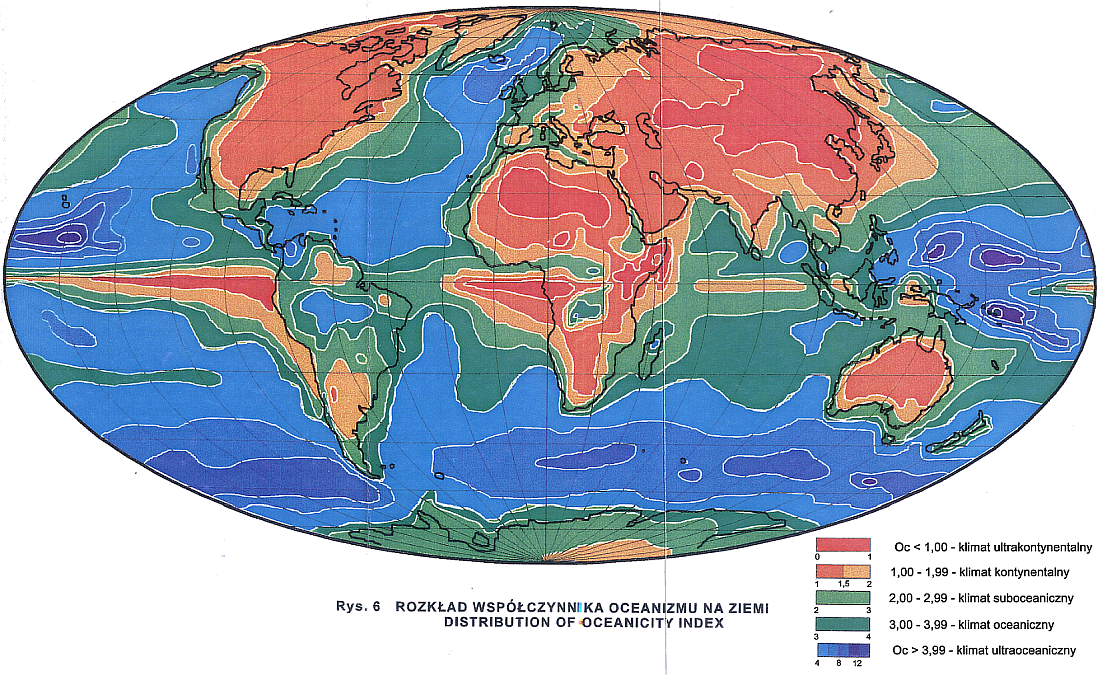
Zdaniem A.A. Marsza, nad lądem każdej z wyróżnionych 5 kategorii klimatu odpowiada określona częstość występowania mas atmosferycznych:

  • tam, gdzie nad lądem zaznacza się zasięg klimatu ultraoceanicznego (Oc > 3,99) występują wyłącznie lub prawie wyłącznie masy morskie świeże, czyli powietrze morskie, które nie uległo procesom transformacji. Taka sytuacja możliwa jest praktycznie nad mniejszymi wyspami oraz w stosunkowo wąskiej strefie wybrzeża. Większy zasięg tego typu klimatu nad obszarami lądowymi może być spowodowany współdziałaniem czynnika cyrkulacyjnego z efektem orograficznym niezbyt wysokich gór (np. Szkocja). W strefie międzyzwrotnikowej, nad lądami, w tej kategorii klimatu przez cały rok występuje powietrze równikowe, którego nie różnicuje się na morskie i kontynentalne ze względu na zasoby pary wodnej;
  • w kategorii klimatu oceanicznego (3,00 ≤ Oc ≤ 3,99) w strukturze występujących mas w ciągu całego roku dominują nieprzetransformowane masy powietrza morskiego, a udział mas innego charakteru jest niewielki. Z innych mas będą to przede wszystkim masy powietrza morskiego starego. Masy powietrza kontynentalnego występować będą epizodycznie i poza strefą przyrównikową (gdzie zaznacza się zmiana położenia MSZ) bez żadnej zaznaczającej się wyraźnie rytmiki sezonowej;
  • w klimacie suboceanicznym (2,00 ≤ Oc ≤ 2,99) w ciągu całego roku przeważają masy powietrza morskiego i morskiego starego, przy czym powietrze morskie stare jest tam masą występującą najczęściej. Masy powietrza kontynentalnego występują głównie latem, przy czym udział mas powietrza kontynentalnego nie przekracza 50%. Na niektórych obszarach (np. w basenie Morza śródziemnego) masy powietrza kontynentalnego występujące latem mogą być masami powoli transformującymi się w masy morskie. W chłodnej porze roku zaznacza się w tym klimacie dominacja mas powietrza morskiego i morskiego starego;
  • w klimacie kontynentalnym (1,00 ≤ Oc ≤ 1,99) obraz częstości występowania mas atmosferycznych jest bardziej skomplikowany. Najbardziej typowym obrazem struktury występujących mas jest zdecydowana przewaga powietrza kontynentalnego nad powietrzem morskim i morskim starym. Część mas powietrza kontynentalnego  występującego nad tymi obszarami stanowi efekt transformacji mas powietrza morskiego w powietrze kontynentalne, w związku z czym zachowuje jeszcze śladowe cechy swojego pierwotnego morskiego pochodzenia. Na niektórych obszarach w tym typie klimatu, na tle ogólnej dominacji kontynentalnych mas atmosferycznych (zwłaszcza w chłodnej porze roku), może zaznaczać się sezonowo zwiększony udział, lub nawet sezonowa dominacja, mas powietrza morskiego starego lub powietrza morskiego intensywnie transformującego się w powietrze kontynentalne przy znacznym udziale konwekcji. Ta ostatnia sytuacja ma miejsce na obszarach, na których występuje cyrkulacja monsunowa lub pseudomonsunowa (np. wschodnie wybrzeże USA, rosyjski Daleki Wschód, rejon Zatoki Gwinejskiej, Indie, …). W każdym jednak przypadku zaznacza się w tym typie klimatu zdecydowana dominacja mas powietrza kontynentalnego w porze zimowej i przejściowych porach roku (jeśli takie występują); 
  • w klimacie ultrakontynentalnym (Oc < 1,00) w ciągu całego roku występują wyłącznie masy powietrza kontynentalnego, którego pochodzenie może być dwojakie. Mogą to być masy powietrza zstępujące z górnych warstw troposfery i na miejscu nabierające właściwości od podłoża. Mogą to być również masy pochodzące z adwekcji, które na swojej drodze nad podłożem lądowym uległy całkowitemu przetransformowaniu w masy kontynentalne, tak że jakiekolwiek ślady ich pierwotnego morskiego pochodzenia są praktycznie niedostrzegalne.

     Zdaniem A.A. Marsza między wartością wskaźnika oceanizmu Oc i częstością występowania mas powietrza morskiego i kontynentalnego występują ściślejsze związki statystyczne o charakterze przyczynowym. Analiza częstości występowania w ciągu roku mas powietrza kontynentalnego na kilku stacjach pozwoliła oszacować częstość występowania mas powietrza kontynentalnego na podstawie wielkości wskaźnika oceanizmu Oc. Jak wynika z analiz A.A. Marsza, gdy Oc < 4,00, to między wskaźnikiem oceanizmu i częstością występowania mas powietrza kontynentalnego (MK), wyrażoną w % czasu roku, zachodzi ścisły związek: MK (%) = 166,66 – 75 · Oc + 8,33 · Oc2, który pozwala określić również częstość występowania w roku mas powietrza morskiego (MM = 100 – MK) ze średnim błędem estymacji ±3,4%. Znając więc wielkość Oc dla danej stacji lądowej można wnioskować o częstości występowania nad nią w ciągu roku mas powietrza kontynentalnego i morskiego. Mając jednak na względzie duży stopień subiektywizmu towarzyszący identyfikacji mas atmosferycznych oraz różnice metodyczne w podejściu do identyfikacji mas (kierunek adwekcji, właściwości fizyczne masy, stopień transformacji) trudno oczekiwać pełnej zgodności między statystykami częstości występowania mas atmosferycznych podawanych przez różnych autorów, a wielkością obliczoną z podanego wyżej wzoru.

     Tego rodzaju tłumaczenie, wyjaśniające związki między częstością występowania mas atmosferycznych i kształtowaniem się wskaźnika Oc, względnie precyzyjne dla obszarów lądowych, dla obszarów oceanicznych może być słuszne tylko częściowo. Jest sprawą oczywistą, że na oddalonych od wybrzeży kontynentów obszarach oceanicznych występować mogą wyłącznie masy powietrza morskiego świeżego, gdyż niezależnie od kierunku cyrkulacji atmosferycznej, masy pochodzenia lądowego muszą w trakcie drogi nad oceanem ulec całkowitej transformacji w powietrze morskie. Tym niemniej, nawet na obszarach oddalonych od wybrzeży, na których występuje typ klimatu ultraoceanicznego, zaznacza się silne zróżnicowanie wielkości wskaźnika Oc (od 4,00 do ponad 12,00). Z kolei, również na obszarach oddalonych od brzegów (na przykład w strefie położonej na południe od równika na wschodnim Pacyfiku), występują powierzchnie, na których Oc jest mniejszy od jedności, co pozwala zakwalifikować (w świetle przyjętych kryteriów podziału) klimat tego akwenu jako ultrakontynentalny. Z całą pewnością nad tym akwenem nie występują masy powietrza kontynentalnego. Nad powierzchniami oceanów (nie mórz wewnętrznych) wskaźnik Oc nie charakteryzuje częstości występowania mas powietrza morskiego, ale oddaje intensywność wymiany cieplnej między powierzchnią oceanu i atmosferą, która pociąga za sobą szereg dalszych skutków o charakterze klimatycznym nad samymi powierzchniami morskimi, jak i poprzez działanie w tym systemie cyrkulacji atmosferycznej – nad obszarami lądowymi.
     Ponieważ przenos ciepła odbywa się również na drodze substancjalnej – poprzez parowanie – wskaźnik oceanizmu Oc charakteryzuje także przenos wilgoci z oceanu do atmosfery. W przypadku gdy nad oceanem wartość wskaźnika Oc jest typowa dla klimatu „utrakontynentalnego” lub „kontynentalnego”, przepływ ciepła jawnego z powierzchni oceanu do atmosfery jest niewielki, ograniczony w swoim rozmiarze jest również przepływ utajonego ciepła parowania (tym samym transfer pary wodnej do atmosfery). Wraz ze wzrostem wartości wskaźnika Oc, obie te wartości rosną, z tym że rozmiar utajonego ciepła parowania ograniczony jest „od góry” przez temperaturę powierzchni morza (Tw), która określa wartość maksymalnej prężności pary wodnej w temperaturze powierzchni oceanu (w warunkach, gdy Tw jest wyższa od temperatury powietrza). To skutkuje, że w wysokich szerokościach geograficznych strumień ciepła jawnego z powierzchni oceanu staje się większy od strumienia utajonego ciepła parowania. Tym czasem w tropikach i subtropikach przez cały rok, a w strefie umiarkowanej w okresie chłodnego półrocza, strumień ciepła jawnego do atmosfery jest wielokrotnie mniejszy od strumienia ciepła parowania.

     Właściwości wskaźnika oceanizmu wskazują, że stanowi on zarówno miarę o charakterze ilościowym, jak i jakościowym, pomocną dla określenia wielkości i intensywności procesu przenosu ciepła i wilgoci w atmosferze. Z tego względu wskaźnik Oc jest wielkością charakteryzującą głównie dynamikę. Mimo, że wskaźnik Oc stanowi miarę opartą na elemencie termiki powietrza, jaką jest roczna amplituda temperatury, nie stanowi bynajmniej miary termiki, lecz miarę o wysokim stopniu kompleksowości klimatycznej. Powoduje to, że wykazuje dość ścisłe korelacje z wieloma parametrami klimatycznymi. Wskaźnik Oc pozwala na wyrobienie sobie poglądu na charakter funkcjonujących na danym obszarze procesów klimatotwórczych. Stanowi on również prostą miarę klimatycznego współoddziaływania w systemie ocean - atmosfera - kontynenty.


Prace, w których wykorzystano wskaźnik oceanizmu Oc (Marsz oceanity index – MOI):

1993 – Marsz A.A. – Wskaźnik oceanizmu termicznego jako miara klimatycznego współoddziaływania w systemie ocean – atmosfera – kontynenty. [w:] Działalność naukowa prof. Władysława Gorczyńskiego i jej kontynuacja. Sympozjum UMK, 16-17.09. Toruń, Streszczenia referatów, s.77-80.

1995 – Marsz A.A. – Rozkład wielkości wskaźnika oceanizmu termicznego na obszarze Arktyki. Problemy Klimatologii Polarnej, 5, s. 11-19 PDF

1995 – Marsz A.A. – Wskaźnik oceanizmu termicznego jako miara klimatycznego współoddziaływania w systemie ocean – atmosfera – kontynenty. Wyższa Szkoła Morska, Wydział Nawigacyjny, Katedra Meteorologii i Oceanografii Nautycznej, Gdynia, s. 1-110. Summary

1995 – Styszyńska A. – Kształtowanie się wskaźnika oceanizmu w rejonie Półwyspu Antarktycznego i Morza Weddella. [w:] Jedność środowiska przyrodniczego Arktyki i Antarktyki. XXII Sympozjum Polarne. Zamek Książ, 27-28 X 1995, s. 159-166.

1996 – Styszyńska A. – Zmiany cyrkulacji atmosferycznej w rejonie Półwyspu Antarktycznego i Morza Weddella w świetle kształtowania się przestrzennych zmian wskaźnika oceanizmu. Problemy Klimatologii Polarnej, 6, s. 213-242. PDF

1998 – Styszyńska A. – Wskaźnik oceanizmu termicznego na obszarze Antarktyki. Problemy Klimatologii Polarnej, 3 (1993, druk w 1998 r.), s. 69-76. PDF

1999 – Marsz A.A. Styszyńska A. – Zmienność częstości występowania mas powietrza morskiego na obszarze północnej i środkowej Polski w XVIII, XIX i XX wieku – przyczyny i konsekwencje. [w:] Zmiany i zmienność klimatu Polski, ich wpływ na gospodarkę, ekosystemy i człowieka. Ogólnopolska Konferencja Naukowa  Łódź, 4–6 listopada 1999, s. 165-170.

2000 – Marsz A.A. – Kontynentalizm i oceanizm klimatu. [w:] Główne cechy klimatu rejonu Polskiej Stacji Antarktycznej im. H. Arctowskiego (Antarktyka Zachodnia, Szetlandy Południowe, Wyspa Króla Jerzego). Wydawnictwo Akademii Morskiej, Gdynia, s. 171-173.

2000 – Marsz A.A., Styszyńska A. – Fazy kontynentalizacji i oceanizacji klimatu nad obszarem Bałtyku w XIX i XX wieku. Acta Universitatis Nicolai Copernici, Geografia, XXXI, s. 183-201. PDF

2000 – Marsz A.A., Styszyńska A. – Variability to the frequency of occurrence of masses of maritime air over Northern and Central Poland in the 18th to 20th centuries. Geographia Polonica, 73, 2, Autumn 2000, s. 127-133. PDF

2002 – Marsz A.A. – Wskaźnik oceanizmu termicznego jako miara klimatycznego współoddziaływania w systemie ocean – atmosfera  kontynenty. [w:] Działalność naukowa profesora Władysława Gorczyńskiego i jej kontynuacja. Sympozjum Klimatologiczne na Uniwersytecie Mikołaja Kopernika, Toruń, 16-17 IX 1993, s. 285-297.

2002 – Styszyńska A., Zblewski S. – Przebieg wartości wskaźnika oceanizmu na Szetlandach Południowych według zweryfikowanych danych połączonego ciągu Deception-Bellingshausen (1944-2000). Problemy Klimatologii Polarnej 12, s. 21-32. PDF

2007 – Marsz A.A. – Kontynentalizm i oceanizm. [w:] Klimat rejonu Polskiej Stacji Polarnej w Hornsundzie – stan, zmiany i ich przyczyny. Wydawnictwo Akademii Morskiej, Gdynia, s. 237-237.

2007 – Styszyńska A. – Zmiany oceanizmu klimatu na obszarze wokółbałtyckim w II połowie XX wieku. [w:] Wahania klimatu w różnych skalach przestrzennych i czasowych. IGiGP Uniwersytetu Jagiellońskiego, Kraków, s.135-143. PDF

2009 – Rachlewicz G. – Contemporary sediment fluxes and relief changes in high Arctic glacierized valley systems (Billefjorden, Central Spitsbergen). Wydawnictwo Naukowe UAM, Poznań, s. 1-203. PDF

2013 – Marsz A.A., Continentality and oceanity of the climate. [w:] Climate and Climate Change at Hornsund, Svalbard. Editors: A.A. Marsz and A. Styszyńska, The publishing house of Gdynia Maritime University, Gdynia, s. 253-255. PDF

2013 – Gadivala M.S., Burke F., Alam M.T., Nawaz-ul-Huda S., Azam M. – Oceanity and continentality climate indices in Pakistan. Geografia Online. Malaysian Journal of Society and Space, 9 (4); 57-66. ISSN 2180-2491 PDF

2013 – Zblewski S., Marsz A.A. – Przebieg wartości wskaźnika oceanizmu w rejonie Cieśniny Beringa w drugiej połowie XX i na początku XXI wieku. Problemy Klimatologii Polarnej 23, s. 57-76. PDF

2014 – Przybylak R., Araźny A., Nordli Ø., Finkelnburg R., Kejna M., Budzik T., Migała K., Sikora S., Puczko D., Rymer K., Rachlewicz G. – Spatial distribution of air temperature on Svalbard during 1 year with campaign measurements. International Journal of Climatology, Vol. 34, Issue 14, s. 3702-3719. PDF

2014 – Styszyńska A. – Przebieg wskaźnika oceanizmu w eurazjatyckim sektorze Arktyki i Subarktyki w XX i na początku XXI wieku. Problemy Klimatologii Polarnej, 24, s. 51-72. PDF

2015 – Andrade C., Corte-Real J. – Spatial distribution of climate indices in the Iberian Peninsula. AIP Conference Proceedings 1648, 110006 (2015); doi: 10.1063/1.4912413 (http://dx.doi.org/10.1063/1.4912413). PDF

2015 – Witek M., Bednorz E., Forycka-Ławniczak H. – Kontynentalizm termiczny w Europie. Badania Fizjograficzne, 6 - ser. A  - Geografia Fizyczna (A66); 171-182. DOI 10.14764/bgf.2015.5.6.13 PDF

2016 – El Kenawy A., McCabe M., Vicente-Serrano S., Robaa S., Lopez-Moreno J. – Recent changes in continentality and aridity conditions over the Middle East and North Africa region, and their association with circulation patterns. Climate Research, Vol. 69: 25-43. (http://dx.doi.org/10.3354/cr01389) PDF

2017 – Andrade C., Corte-Real J. – Assessment of the spatial distribution of continental-oceanic climate indices in the Iberian Peninsula. International Journal of Climatology, Vol. 37, Issue 1, s. 36-45. (https://doi.org/10.1002/joc.4685)

2018 – Bochenek W., Kijowska-Strugała M., Kiszka K. – Wieloletnie tendencje warunków klimatycznych w Szymbarku na podstawie wybranych wskaźników. Przegląd Geograficzny, 90, z.1, s.35-52. PDF

2018 – Sánchez-Salguero R., Camarero J.J., Roza V., Génova M., Olano J.M., Erzac A., Gazol A., Caminero L., Tejedor E., de Luis M., Linares J.C. – Resist, recover or both? Growth plasticity in response to drought is geographically structured and linked to intraspecific variability in Pinus pinaster. Journal of Biogeography, Vol. 45, Issue 5, s. 1126-1139. PDF

2018 – Vlăduţ A., Nikolova N., Licurici M. – Evaluation of thermal continentality within southern Romania and northern Bulgaria (1961–2015). Geofizika, Vol. 35, s. 1-18, DOI: 10.15233/gfz.2018.35.1 PDF

2020 – Zepeda Rivas D., Rodriges Alvarez J., Loonen R. – Building performance, climatic variables, and indices: identification of correlations for social housing across the Mexican territory. [w:] Proceedings of PLEA. PDF

2022 – Przybylak R., Wyszyński P., Araźny A. – Comparison on Early-Twentieth-Century Arctic Warming and Contemporary Arctic Warming in the Light of Daily and Subdaily Data. Journal of Climate, Vol. 35, Issue 7, s. 2269-2290. PDF
 

.